1.9. Range (Image) and Column Space

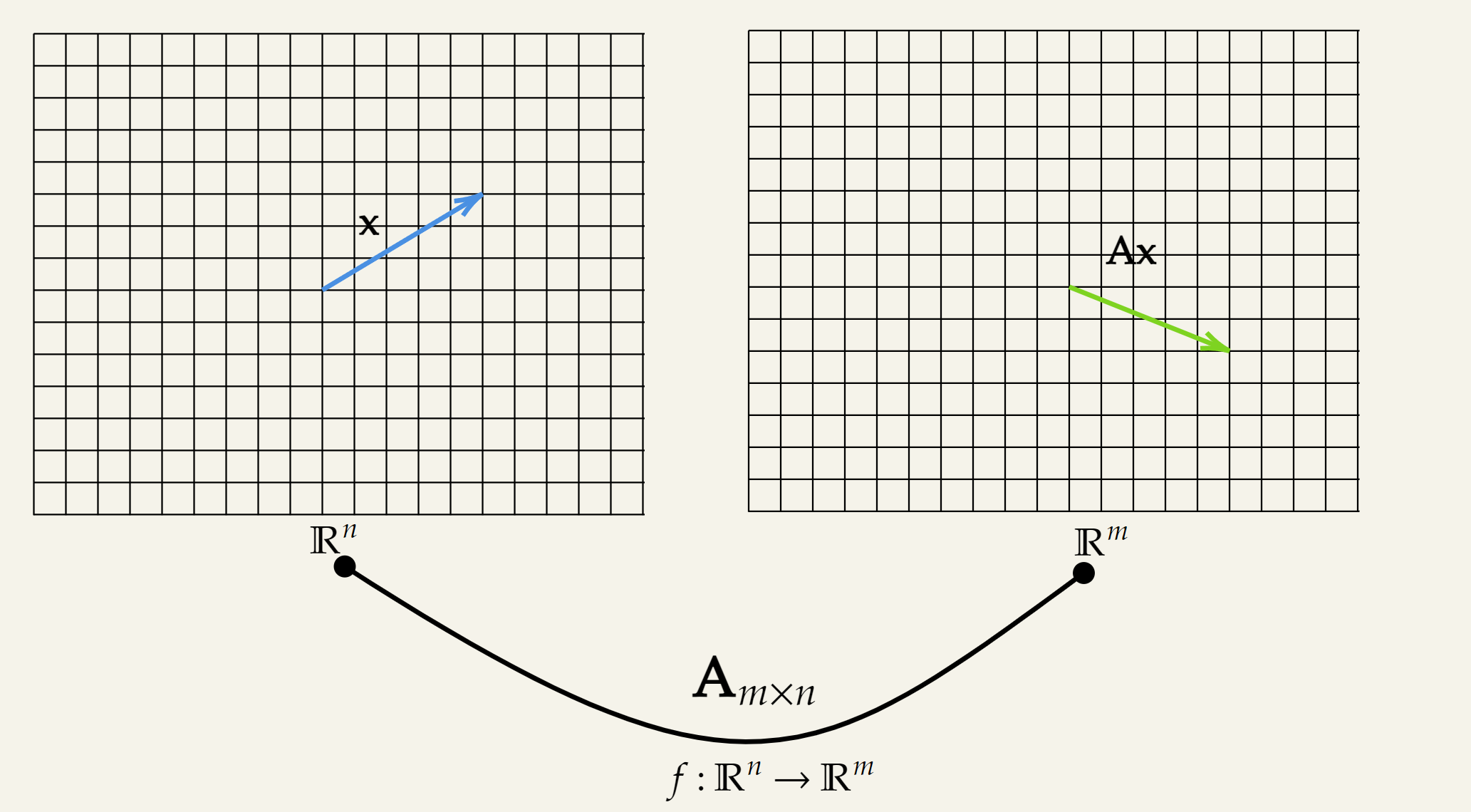
Let’s start with the definition. Consider a matrix $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ and recall the intuition behind $\mathbf{Ax}$ from Matrix Vector Multiplication, especially the functional transform perspective.

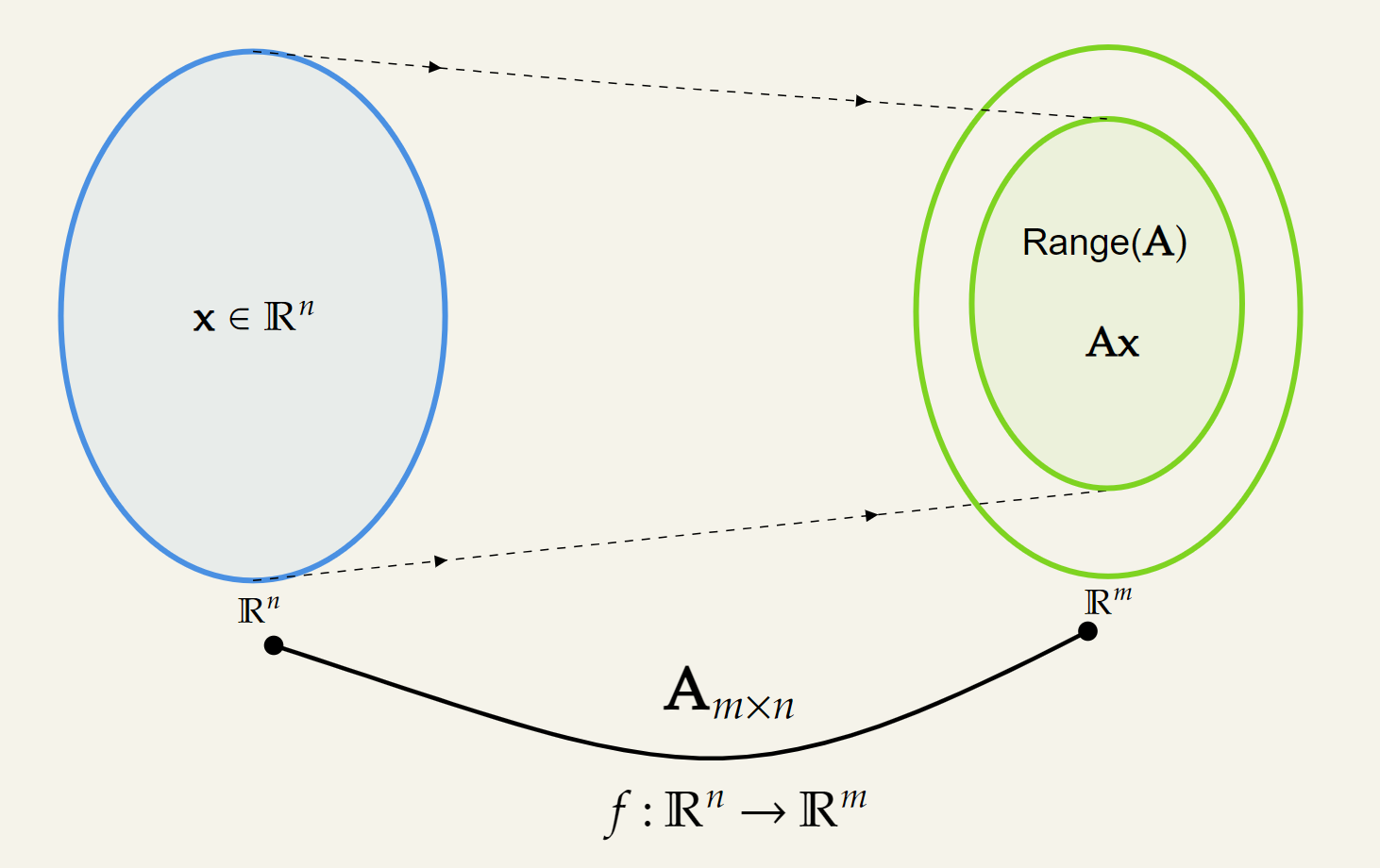
Based on this we can define the range (also known as the image) of a matrix transformation as follows:

$$\text{Range}(\mathbf{A}):=\{\mathbf{Ax}\mid \mathbf{x}\in {\mathbb{R}}^n\}\subseteq {\mathbb{R}}^m$$

Interpretation:

• All the vectors $\mathbf{x}$ in ${\mathbb{R}}^n$ are going through the transformation $\mathbf{Ax}$.
• After going through the transformation, every vector $\mathbf{x}$ in ${\mathbb{R}}^n$ is getting mapped to a subspace in ${\mathbb{R}}^m$.
• That particular subspace in ${\mathbb{R}}^m$ is called the Range of $\mathbf{A}$ (or the Image of $\mathbf{A}$). A nice way to interpret this is with the Venn diagrams of the vector space of ${\mathbb{R}}^n$ and ${\mathbb{R}}^m$.

This means range is the subspace where the vectors get mapped to after the transformation. Consider the following equation:

$$\mathbf{Ax}=\mathbf{b}$$

Here, if we consider every possible $\mathbf{x}$, the generated $\mathbf{b}$ vectors construct a subspace. That subspace is the range (or image) of $\mathbf{A}$.

Connecting to Column space §

Based on Matrix Vector Multiplication discussion, we can intuit that, the subspace we are talking about when we say $\text{Range}(\mathbf{A})$ is actually the column space of $\mathbf{A}$.

Because $\mathbf{Ax}$ can be interpreted as the linear combination of the columns of $\mathbf{A}$. That means, by taking the linear combination of columns of $\mathbf{A}$, we are forming a subspace which is known as the column space. And, the name is self-explanatory because the subspace is constructed by taking the linear combination of columns of $\mathbf{A}$.

We can also relate this to the idea of Span.

$$\mathbf{A}=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{a}}_1& {\mathbf{a}}_2& \dots & {\mathbf{a}}_n\\ \mid & \mid & & \mid \end{array}\right]$$

The subspace that is spanned by the columns of $\mathbf{A}$ is the column space. Mathematically,

$$\mathrm{Range}(\mathbf{A})=\mathrm{span}({\mathbf{a}}_1,{\mathbf{a}}_2,\cdots ,{\mathbf{a}}_n)$$

All of the following can be thought of equivalent: $\mathrm{Col}(\mathbf{A})\equiv \mathrm{Range}(\mathbf{A})\equiv \mathrm{Im}(\mathbf{A})$