1.5. Subspaces

Definition §

A subspace $W$ of a vector space is a subset with special closure property. Formally, a subspace $W\subseteq {\mathbb{C}}^n$ is a set that is closed under addition operation ($+$) and scalar multiplication.

Though it is not explicitly mentioned, all subspaces considered are linear subspaces.

Properties that need to hold for a valid subspace:

• $0$ is included in the subspace.

$$0=\left[\begin{array}{c}0\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]\in W$$

• For all, ${\mathbf{v}}_1,{\mathbf{v}}_2\in W$; ${\mathbf{v}}_1+{\mathbf{v}}_2\in W$. This means the subspace is closed under addition operation. In other words, if we pick any two vectors from the subspace, the resultant vector from the addition of those two vectors is also in the subspace.
• For all $\mathbf{v}\in W$ and $\alpha \in \mathbb{C}$; $\alpha \mathbf{v}\in W$. This means the subspace is closed under scalar multiplication.

The subspace must be a non-empty set.

Visual Intuition of Subspaces §

Even though subspaces are quite a general concept, it’s good to get some visual intuition in lower dimensions.

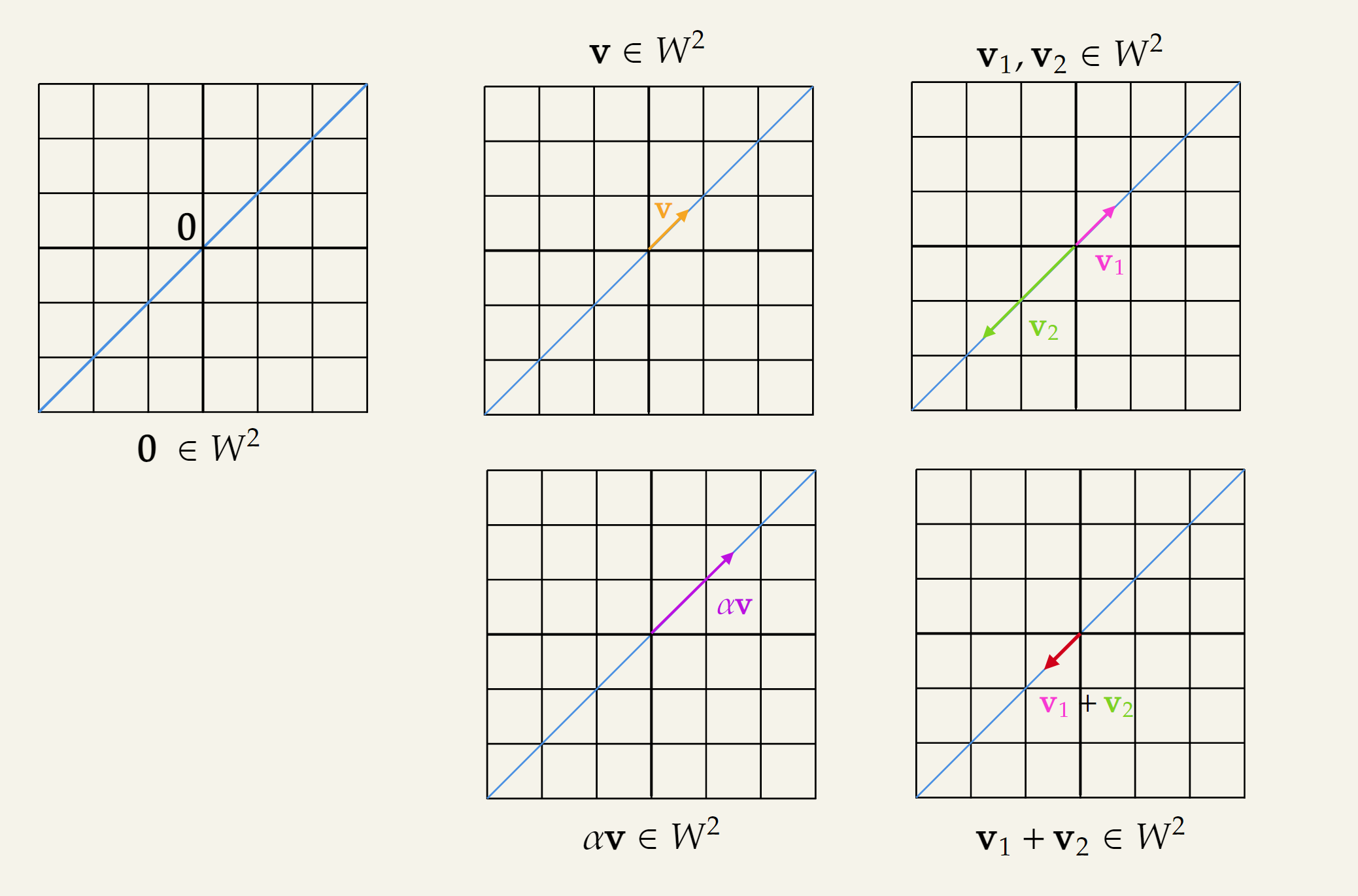
Consider the following diagram which shows a subspace ${\mathbb{W}}^2$ for a vector space in ${\mathbb{R}}^2$. In such a case, the subspace is an infinite line going through the origin. As it goes through the origin, the $0$ is included in the subspace. In addition, it follows the other two criteria also.

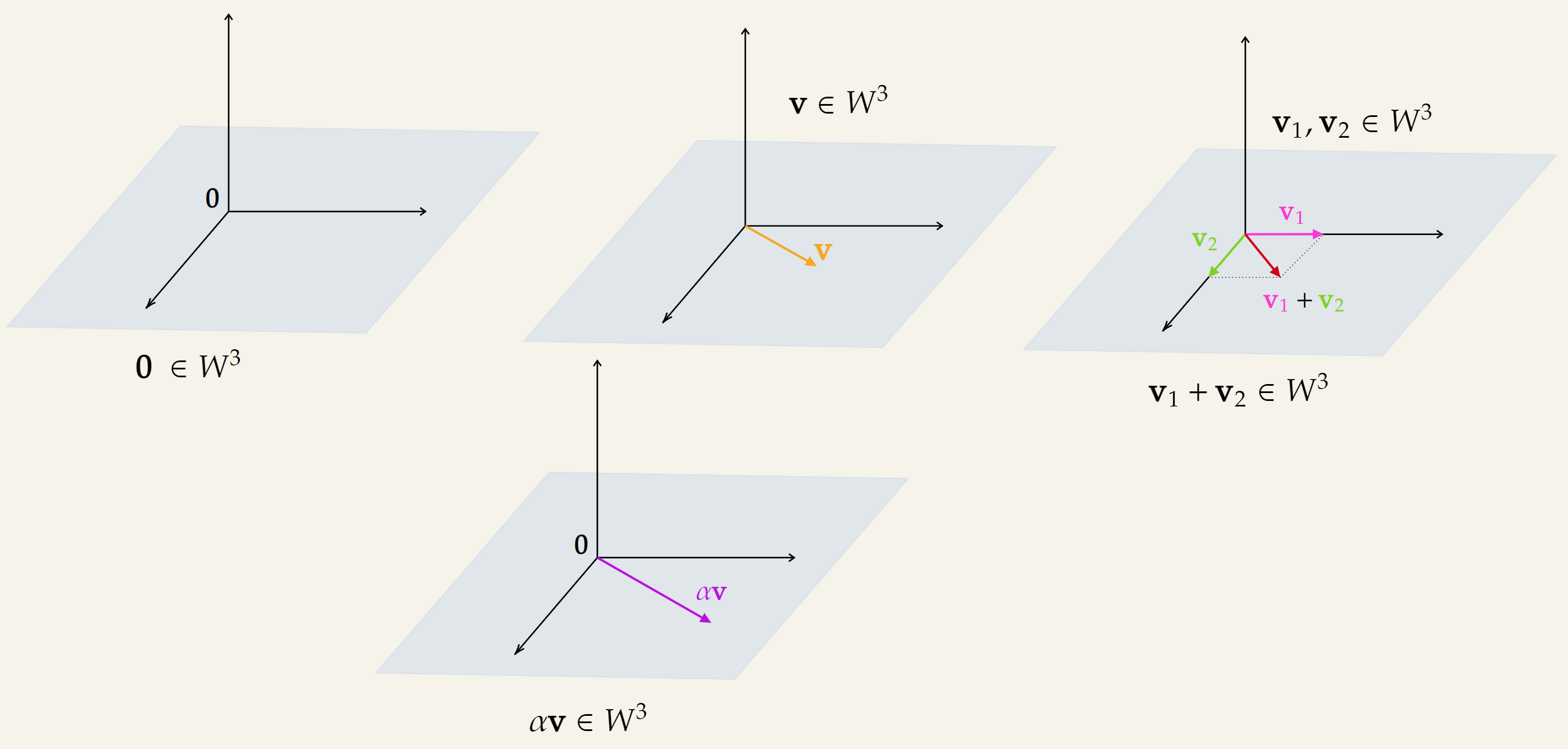
For a vector space in ${\mathbb{R}}^3$, a valid subspace is an infinite plane going through the origin. A visualization is given below:

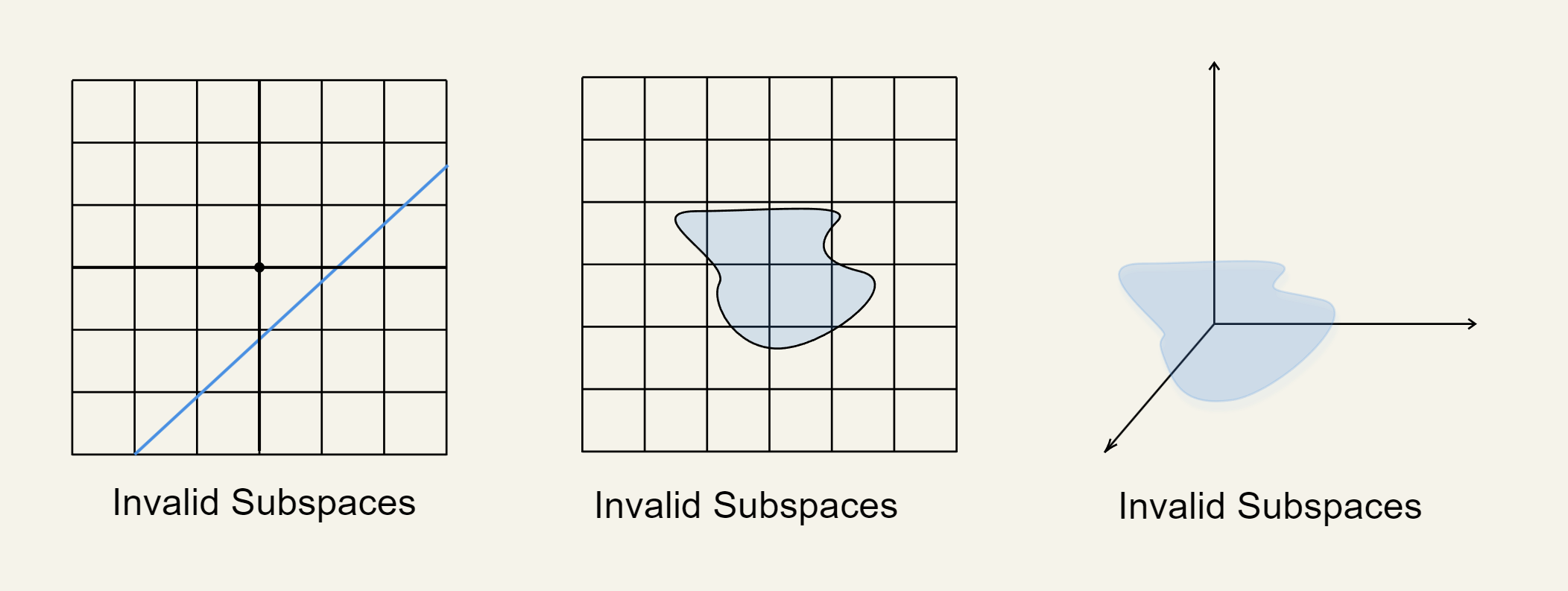
One example of an invalid subspace is an affine subspace which is an infinite line that does not go through the origin. Also, based on the geometric intuition mentioned above, we can easily visualize some other examples of invalid subspaces.