1.1. Matix Vector Multiplication

Consider a matrix $\mathbf{A}\in {\mathbb{C}}^{m\times n}$ and a vector $\mathbf{x}\in {\mathbb{C}}^n$.

$$\mathbf{A}:=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{a}}_1& {\mathbf{a}}_2& \dots & {\mathbf{a}}_n\\ \mid & \mid & & \mid \end{array}\right]$$

where, ${\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_n$ are columns of matrix $\mathbf{A}$.

$$\mathbf{x}:=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$$

There are several ways we can interpret the Matrix vector multiplication.

Linear Combination of Columns of Matrix §

---

A way to express it is scaling the columns of $\mathbf{A}$ with the elements of vector $\mathbf{x}$.

$$\begin{array}{rl}\mathbf{Ax}& =\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{a}}_1& {\mathbf{a}}_2& \dots & {\mathbf{a}}_n\\ \mid & \mid & & \mid \end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]\\ & \\ & =x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+\dots +x_n{\mathbf{a}}_n\end{array}$$

This can be written in a much more compact form as follows:

$$\mathbf{Ax}=x_1{\mathbf{a}}_1+x_2{\mathbf{a}}_2+\dots +x_n{\mathbf{a}}_n=\sum _{i=1}^n{x}_i{\mathbf{a}}_i$$

This is nothing but a linear combination of the columns of matrix $\mathbf{A}$.

Functional Transformation Perspective §

---

We can interpret the matrix-vector multiplication through the lens of functions.

Consider a function $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ and the matrix-vector multiplication can be thought of as the following transformation:

$$f(\mathbf{x}):=\mathbf{Ax}$$

To put it into words, we are plugging in a vector $\mathbf{x}\in {\mathbb{R}}^n$ which results in applying a transformation defined by a matrix $\mathbf{A}\in {\mathbb{R}}^{m\times n}$. The result of the transformation is another vector in ${\mathbb{R}}^m$. This can be further interpreted as a mapping between two vector spaces; from ${\mathbb{R}}^n$ to ${\mathbb{R}}^m$.

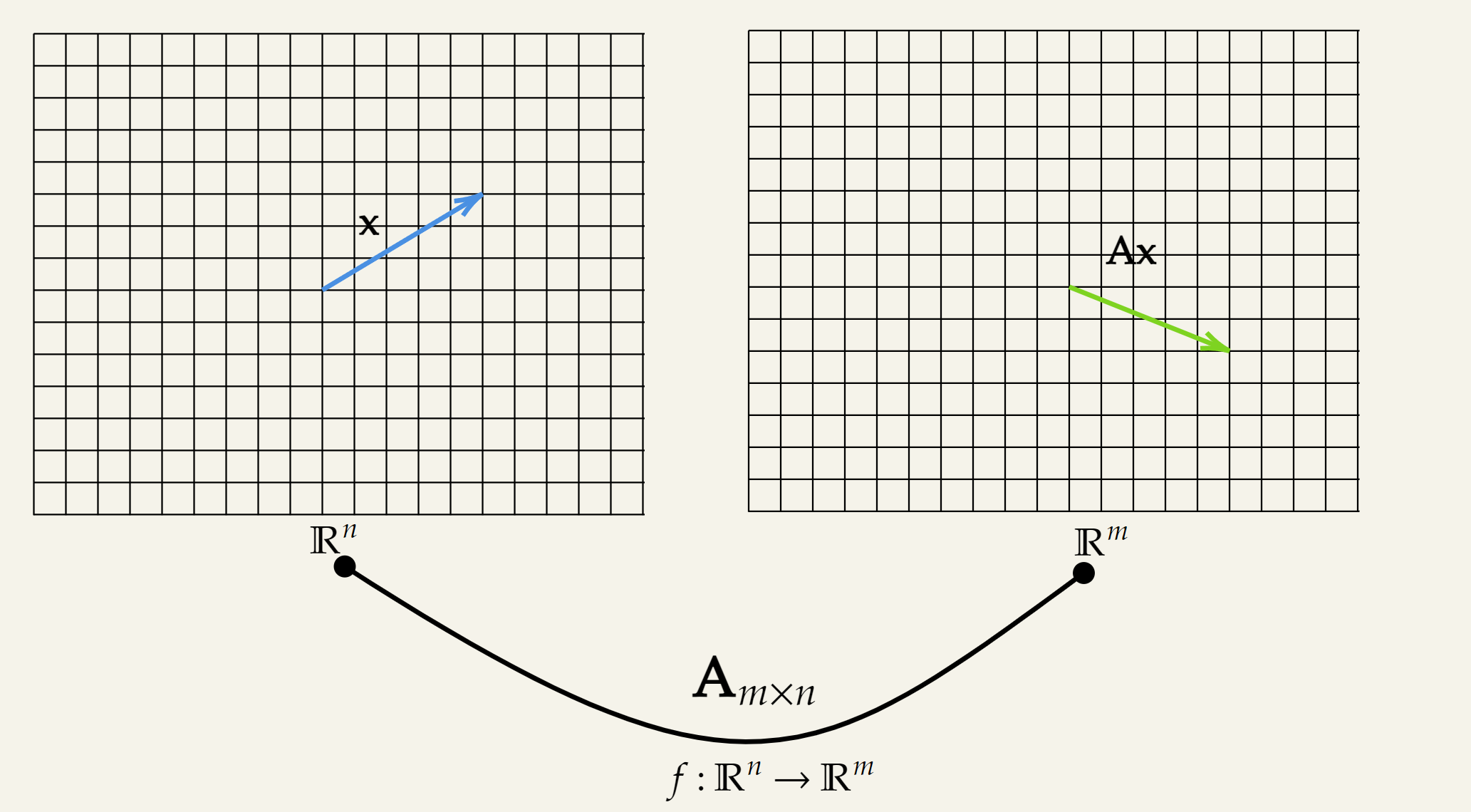
Note that this holds true for $f:{\mathbb{C}}^n\to {\mathbb{C}}^m$ also.

Most of the time we do not separate out the input space and the output space of the function but superimpose them in a single plot. This allows us to visualize the transformation in a single plot.

Now what kind of transformation would it be depends on the nature of the matrix. Visualization and intuition behind these transformations are explained in detail in Matrix Multiplication as Transformation.

Another important thing to mention here, these transformations require one specific property which is the function needs to be linear. In other words, these transformations need to hold the Linearity property.

Establishing the relation with elementary basis vectors §

---

Rather than thinking about the matrix $\mathbf{A}$ transforming the vector $\mathbf{x}$, we can think about it from another perspective. To do this we need to decompose the vector $\mathbf{x}$ into elementary basis vectors.

$$\mathbf{x}=x_1{\mathbf{e}}_1+x_2{\mathbf{e}}_2+\cdots +x_n{\mathbf{e}}_n$$

where, ${\mathbf{e}}_1,{\mathbf{e}}_2,\cdots ,{\mathbf{e}}_n$ are the elementary basis vectors.

For better understanding let’s write out the expression more explicitly,

$$\mathbf{x}=x_1\left[\begin{array}{c}1\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]+x_2\left[\begin{array}{c}0\\ 1\\ 0\\ ⋮\\ 0\end{array}\right]+x_3\left[\begin{array}{c}0\\ 0\\ 1\\ ⋮\\ 0\end{array}\right]+\dots +x_n\left[\begin{array}{c}0\\ 0\\ 0\\ ⋮\\ 1\end{array}\right]$$

Visualize this as decomposing the vector $\mathbf{x}$ into it’s elementary basis vectors. Each elementary basis vector is getting scaled by $x_1$, $x_2,\dots ,x_n$ and summed up to form the vector $\mathbf{x}$.

Now, when we multiply the matrix with the vector $\mathbf{x}$, what actually gets transformed is the “elementary basis vectors”. Let’s see it mathematically

$$\begin{array}{rl}\mathbf{Ax}& =\mathbf{A}(x_1{\mathbf{e}}_1+x_2{\mathbf{e}}_2+\cdots +x_n{\mathbf{e}}_n)\\ & =x_1\mathbf{A}{\mathbf{e}}_1+x_2\mathbf{A}{\mathbf{e}}_2+\dots +x_n\mathbf{A}{\mathbf{e}}_n\end{array}$$

Note from going to the first line to the second line requires a strong assumption which is Linearity.

Think of $\mathbf{A}{\mathbf{e}}_{\mathbf{i}}$ as just applying the transformation defined by matrix $\mathbf{A}$ to the elementary basis vector ${\mathbf{e}}_{\mathbf{i}}$. But notice what happens when we actually go through the computation:

$$\mathbf{A}{\mathbf{e}}_1=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{a}}_1& {\mathbf{a}}_2& \dots & {\mathbf{a}}_n\\ \mid & \mid & & \mid \end{array}\right]\left[\begin{array}{c}1\\ 0\\ 0\\ ⋮\\ 0\end{array}\right]={\mathbf{a}}_1$$ $$\mathbf{A}{\mathbf{e}}_2=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{a}}_1& {\mathbf{a}}_2& \dots & {\mathbf{a}}_n\\ \mid & \mid & & \mid \end{array}\right]\left[\begin{array}{c}0\\ 1\\ 0\\ ⋮\\ 0\end{array}\right]={\mathbf{a}}_2$$ $$⋮$$ $$\mathbf{A}{\mathbf{e}}_n=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{a}}_1& {\mathbf{a}}_2& \dots & {\mathbf{a}}_n\\ \mid & \mid & & \mid \end{array}\right]\left[\begin{array}{c}0\\ 0\\ 0\\ ⋮\\ 1\end{array}\right]={\mathbf{a}}_n$$

We are just pulling out the corresponding column (index of ${\mathbf{e}}_i$) of the matrix $\mathbf{A}$. And, we get back the first perspective of the matrix-vector multiplication i.e. linear combination of columns of a matrix.

How to Interpret a Matrix

The columns of matrix $\mathbf{A}$ specify where elementary basis vectors will end up after transformation.

$${\mathbf{e}}_i\to {\mathbf{a}}_i$$

Here, we specifying ${\mathbf{e}}_i$ will be transformed to ${\mathbf{a}}_i$

Inner Product Perspective §

---

For this perspective we need to express the matrix $\mathbf{A}$ as follows:

$$\mathbf{A}:=\left[\begin{array}{ccc}-& {\mathbf{a}}_1^{{\prime }^{\top }}& -\\ -& {\mathbf{a}}_2^{{\prime }^{\top }}& -\\ & ⋮& \\ -& {\mathbf{a}}_n^{{\prime }^{\top }}& -\end{array}\right]$$

Considering this, the matrix-vector multiplication can be expressed as the following:

$$\mathbf{Ax}=\left[\begin{array}{c}{\mathbf{a}}_1^{{\prime }^{\top }}\mathbf{x}\\ {\mathbf{a}}_2^{{\prime }^{\top }}\mathbf{x}\\ ⋮\\ {\mathbf{a}}_n^{{\prime }^{\top }}\mathbf{x}\end{array}\right]$$

Side Note:

In the following discussion, I violated the rule of always considering vectors as column vectors.

Just as a caution, you have to be careful how you write out the matrix $\mathbf{A}$. If it is written in the following form,

$$\mathbf{A}=\left[\begin{array}{ccc}-& {\mathbf{a}}_1^{\prime }& -\\ -& {\mathbf{a}}_2^{\prime }& -\\ & ⋮& \\ -& {\mathbf{a}}_n^{\prime }& -\end{array}\right]$$

Here, ${\mathbf{a}}_1^{\prime }$, ${\mathbf{a}}_2^{\prime },\cdots ,{\mathbf{a}}_n^{\prime }$ are written in row vector format. In this case, for matrix vector multiplication we need to write the inner product explicitly as follows:

$$\mathbf{Ax}=\left[\begin{array}{c}⟨{\mathbf{a}}_1^{\prime },\mathbf{x}⟩\\ ⟨{\mathbf{a}}_2^{\prime },\mathbf{x}⟩\\ ⋮\\ ⟨{\mathbf{a}}_n^{\prime },\mathbf{x}⟩\end{array}\right]$$

References §

---

1. Gundersen, Gregory. Matrices as Functions, Matrices as Data. 28 Aug. 2022, gregorygundersen.com/blog/2022/08/28/matrices-as-functions-and-data/.
2. Bernstein, Matthew. Matrix-vector multiplication. 19 Dec. 2020, mbernste.github.io/posts/matrix_vector_mult.