1.7. Linear Independence

First Definition §

A set of vectors $S=\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_n\}$ is linearly independent if the following is true:

$$\boxed{{\alpha }_1{\mathbf{v}}_1+{\alpha }_2{\mathbf{v}}_2+\cdots +{\alpha }_n{\mathbf{v}}_n=0\text{iff}{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n=0}$$

To interpret this we just need to think about a counter-example. Consider a set of vectors $\{\mathbf{v}{\}}_i$ and another set of vectors $\{\mathbf{v}{\}}_j$ from $S$. Now if the linear combination of the first set of vectors is in direction opposition to the linear combination of vectors of the second set, the summation would result in $0$. That would mean there is a linear dependence. In what scenario there wouldn’t be a linear dependence? If no vector (linear combination of vectors) from $S$ can be expressed as a linear combination of any other vector/vectors.

Example in ${\mathbb{R}}^3$ :

For a concrete example, let’s restrict ourselves to ${\mathbb{R}}^3$ and consider only three vectors i.e. $S=\{{\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3\}$.

$${\alpha }_1{\mathbf{v}}_1+{\alpha }_2{\mathbf{v}}_2+{\alpha }_3{\mathbf{v}}_3=0$$

Case 1: Consider ${\alpha }_1=0$ and ${\alpha }_2,{\alpha }_3\ne 0$,

$$\begin{array}{r}{\alpha }_2{\mathbf{v}}_2+{\alpha }_3{\mathbf{v}}_3=0\\ {\alpha }_2{\mathbf{v}}_2=-{\alpha }_3{\mathbf{v}}_3\end{array}$$

This means ${\mathbf{v}}_2$ and ${\mathbf{v}}_3$ are colinear or in other words lies along the same line. Furthermore, this implies, they are linearly dependent.

Case 2: Consider ${\alpha }_2=0$ and ${\alpha }_1,{\alpha }_3\ne 0$,

$$\begin{array}{r}{\alpha }_1{\mathbf{v}}_1+{\alpha }_3{\mathbf{v}}_3=0\\ {\alpha }_1{\mathbf{v}}_1=-{\alpha }_3{\mathbf{v}}_3\end{array}$$

In this case, ${\mathbf{v}}_1$ and ${\mathbf{v}}_3$ are colinear and linearly dependent.

Case 3: Consider ${\alpha }_3=0$ and ${\alpha }_1,{\alpha }_2\ne 0$,

$$\begin{array}{r}{\alpha }_1{\mathbf{v}}_1+{\alpha }_2{\mathbf{v}}_2=0\\ {\alpha }_1{\mathbf{v}}_1=-{\alpha }_2{\mathbf{v}}_2\end{array}$$

In this case, ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ are colinear and linearly dependent.

Case 4 : Out of ${\alpha }_1,{\alpha }_2,{\alpha }_3$ only one is non-zero and remaining two are zero.

$${\alpha }_1{\mathbf{v}}_1\ne 0$$ $${\alpha }_2{\mathbf{v}}_2\ne 0$$ $${\alpha }_3{\mathbf{v}}_3\ne 0$$

In this case, it is not possible to get a zero vector (without the trivial case).

Case 5: Consider ${\alpha }_1,{\alpha }_2,{\alpha }_3\ne 0$.

$${\alpha }_1{\mathbf{v}}_1+{\alpha }_2{\mathbf{v}}_2=-{\alpha }_3{\mathbf{v}}_3$$ $$\text{or}$$ $${\alpha }_2{\mathbf{v}}_2+{\alpha }_3{\mathbf{v}}_3=-{\alpha }_1{\mathbf{v}}_1$$ $$\text{or}$$ $${\alpha }_1{\mathbf{v}}_1+{\alpha }_3{\mathbf{v}}_3=-{\alpha }_2{\mathbf{v}}_2$$

This implies one of the vectors can be written as a linear combination of the other two vectors i.e. there exists a linear dependence among the vectors.

This means the only way all three vectors will be linearly independent is ${\alpha }_1=0,{\alpha }_2=0,{\alpha }_3=0$. Only in that case, ${\alpha }_1{\mathbf{v}}_1+{\alpha }_2{\mathbf{v}}_2+{\alpha }_3{\mathbf{v}}_3=0$ and all the vectors are linearly independent.

General Version: Consider ${\alpha }_i\ne 0$, we can write the following:

$${\alpha }_i{\mathbf{v}}_i=-{\alpha }_1{\mathbf{v}}_1-{\alpha }_2{\mathbf{v}}_2-\cdots -{\alpha }_{i-1}{\mathbf{v}}_{i-1}-{\alpha }_{i+1}{\mathbf{v}}_{i+1}-\cdots -{\alpha }_n{\mathbf{v}}_n$$

Dividing by ${\alpha }_i$ ,

$${\mathbf{v}}_i=-\frac{1}{{\alpha }_i}({\alpha }_1{\mathbf{v}}_1+{\alpha }_2{\mathbf{v}}_2+\cdots +{\alpha }_{i-1}{\mathbf{v}}_{i-1}+{\alpha }_{i+1}{\mathbf{v}}_{i+1}+\cdots +{\alpha }_n{\mathbf{v}}_n)$$

This implies ${\mathbf{v}}_i$ can be written as the linear combination of other vectors i.e. the set of vectors is linearly dependent.

Second Definition §

Another definition that relates linear independence to the concept of Span is mentioned below. For any vector ${\mathbf{v}}_i\in S$ the following needs to hold true:

$${\mathbf{v}}_i\notin \mathrm{Span}\left(S\backslash \left\{{\mathbf{v}}_i\right\}\right)$$

We can form the definition for linear dependence as follows. For any vector ${\mathbf{v}}_i\in S$ if the following is true:

$${\mathbf{v}}_i\in \mathrm{Span}\left(S\backslash \left\{{\mathbf{v}}_i\right\}\right)$$

This would mean there is a linear dependence between the vectors in $S$. The following visualization shows two such cases, where the set $S$ contains linearly dependent vectors.

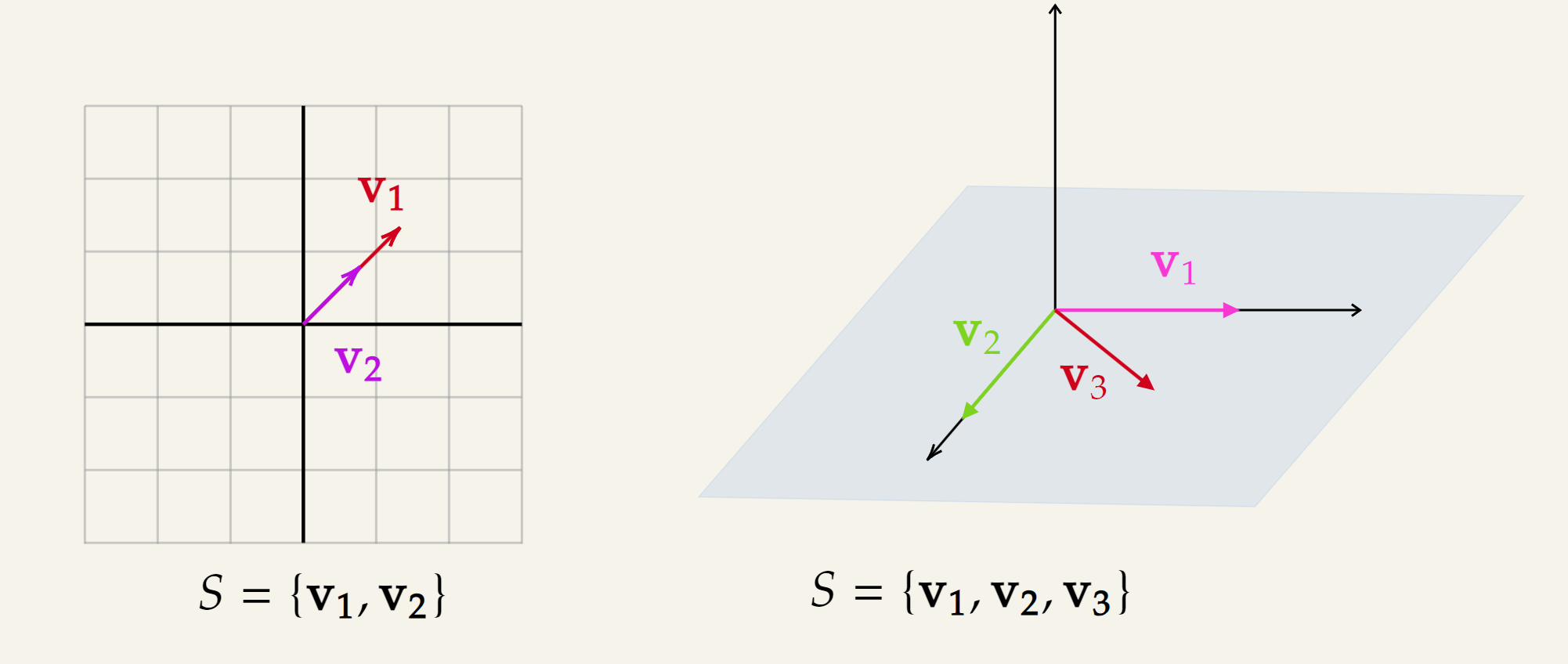
References §

1. Bernstein, Matthew. Span and Linear Independence. 11 June 2022, mbernste.github.io/posts/linear_independence/.
2. Gundersen. Linear Independence, Basis, and the Gram–Schmidt Algorithm. gregorygundersen.com/blog/2021/04/24/linear-independence/.