1.2. Linearity

The concept of linearity is quite a general concept. However, I will keep it limited to linear transformation in the context of functions and matrix multiplications.

Linearity in Functions §

---

Consider a function $f$. For linearity, two different properties need to hold.

• Additivity: $f(x+y)=f(x)+f(y)$
• Homogeneity of degree-1 (Scaling): $f(ax)=af(x)$

Now these two properties can be combined into a single expression that holds if a function is linear:

$$f(\alpha x+\beta y)=\alpha f(x)+\beta f(y)$$

Linearity in terms of Matrix Multiplication §

---

The map $\mathbf{x}\to f(\mathbf{x})$ is linear if for any $\mathbf{x},\mathbf{y}\in {\mathbb{C}}^n$ and any $\alpha \in \mathbb{C}$,

$$\boxed{\begin{array}{rl}& \\ \mathbf{A}(\mathbf{x}+\mathbf{y})& =\mathbf{Ax}+\mathbf{Ay}\\ \mathbf{A}(\alpha \mathbf{x})& =\alpha \mathbf{Ax}\\ & \end{array}}$$

What does it mean intuitively or visually? It is hard to describe its general form. But some properties that need to be preserved in geometric sense:

• After the transformation, the origin of the vector can not be shifted
• Parallel lines stay parallel after transformation.

I will provide two counter-examples where linearity is not preserved.

The following is an example of affine transformations.

$$f(\mathbf{x})=\mathbf{Ax}+\mathbf{b}$$

These kinds of transformations perform an additional “shifting” to the vectors in addition to a linear transformation. Here, the shifting is done by the vector $\mathbf{b}$ and essentially shifts the origin which violates the assumptions of linearity. To summarize, Given a vector $\mathbf{x}$, $\mathbf{Ax}$ is a linear transformation, but when an additional shift $b$ is applied it is no longer linear.

The following is another visualization of how a non-linear transformation may look like.

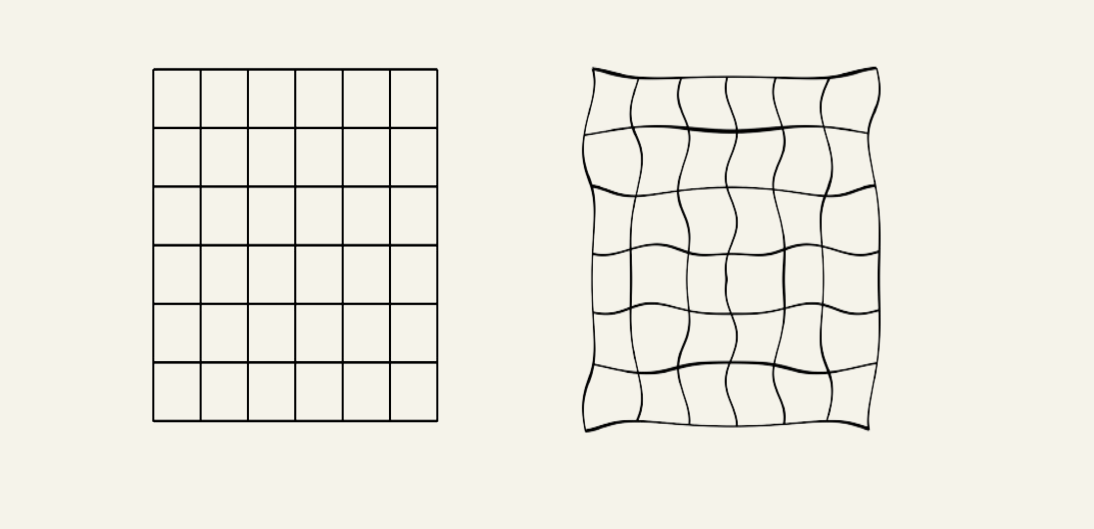
In a purely geometric sense, parallel lines are no longer parallel after the transformation.

Understanding the Linearity in Matrix Multiplication §

---

Let’s define the matrix transformation $\mathbf{A}$ as some functional transformation to the elementary basis vectors of the vector space ${\mathbb{R}}^n$.

$$\mathbf{A}=\left[f({\mathbf{e}}_1)|f({\mathbf{e}}_2)|\cdots |f({\mathbf{e}}_n)\right]$$

What happens when we multiply the matrix $\mathbf{A}$ with a specific basis vector?

$$\begin{array}{rl}\mathbf{A}{\mathbf{e}}_i& =\left[f({\mathbf{e}}_1)|f({\mathbf{e}}_2)|\cdots |f({\mathbf{e}}_n)\right]{\mathbf{e}}_i\\ & =f({\mathbf{e}}_i)\end{array}$$

What happens when we do this for a general vector $\mathbf{x}$,

$$\begin{array}{rl}f(\mathbf{x})& =f\left(\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]\right)\\ & =f(x_1{\mathbf{e}}_1+x_2{\mathbf{e}}_2+\dots +x_n{\mathbf{e}}_n)\end{array}$$

Now assuming the linearity holds we can we write the following

$$\begin{array}{rl}f(\mathbf{x})& =f(x_1{\mathbf{e}}_1+x_2{\mathbf{e}}_2+\dots +x_n{\mathbf{e}}_n)\\ & =x_{1}f({\mathbf{e}}_1)+x_{2}f({\mathbf{e}}_2)+\dots +x_{n}f({\mathbf{e}}_n)\\ & =\left[f({\mathbf{e}}_1)|f({\mathbf{e}}_2)|\cdots |f({\mathbf{e}}_n)\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]\\ & =\left[f({\mathbf{e}}_1)|f({\mathbf{e}}_2)|\cdots |f({\mathbf{e}}_n)\right]\mathbf{x}\\ & =\mathbf{Ax}\end{array}$$