1.4. Matrix Matrix Multiplication

The easiest way to intuit matrix matrix multiplication is as a composition of linear transformations. But before doing that, let’s go through the formal definition.

Consider a matrix $\mathbf{A}\in {\mathbb{C}}^{l\times m}$ :

$$\mathbf{A}=\left[\begin{array}{ccc}-& {\mathbf{a}}_1^{{\prime }^{\top }}& -\\ -& {\mathbf{a}}_2^{{\prime }^{\top }}& -\\ & ⋮& \\ -& {\mathbf{a}}_l^{{\prime }^{\top }}& -\end{array}\right]$$

Consider another matrix $\mathbf{B}\in {\mathbb{C}}^{m\times n}$ :

$$\mathbf{B}=\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{b}}_1& {\mathbf{b}}_2& \dots & {\mathbf{b}}_n\\ \mid & \mid & & \mid \end{array}\right]$$

The resultant matrix $\mathbf{C}\in {\mathbb{C}}^{l\times n}$ can be expressed as follows:

$$\begin{array}{rl}\mathbf{C}& =\mathbf{AB}\\ & =\left[\mathbf{A}{\mathbf{b}}_1|\mathbf{A}{\mathbf{b}}_2|\dots |\mathbf{A}{\mathbf{b}}_n\right]\end{array}$$

Notice that, each column of matrix $\mathbf{B}$ is getting transformed by the matrix $\mathbf{A}$.

Functional Transformation Perspective §

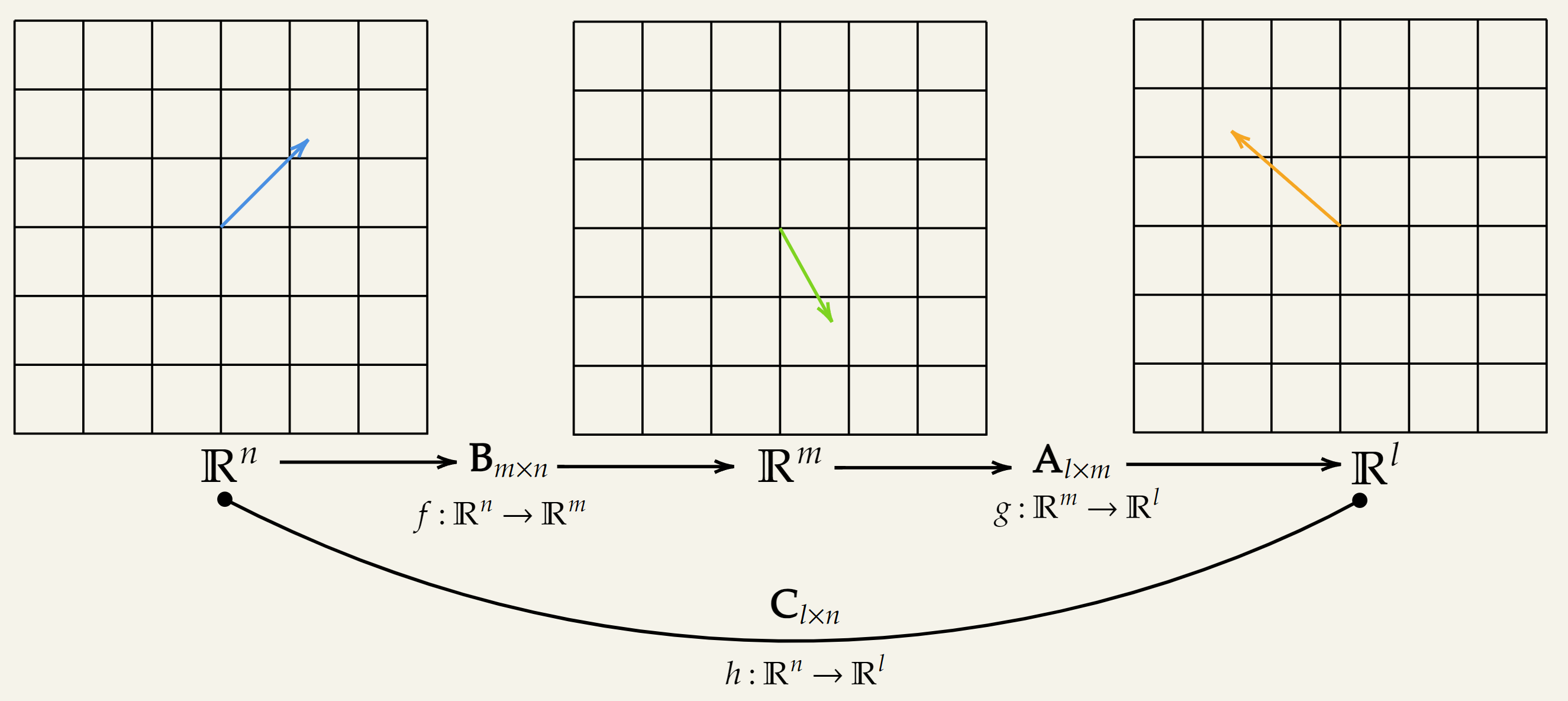
Let’s think about matrix multiplication from a functional transformation perspective. Consider two functions $g:{\mathbb{R}}^m\to {\mathbb{R}}^l$ and $f:{\mathbb{R}}^n\to {\mathbb{R}}^m$ where both functions abide by the Linearity property.

$$\begin{array}{rl}h(\mathbf{x})& =g(f(\mathbf{x}))\\ & =\mathbf{ABx}\end{array}$$

where, $g\circ f=h:{\mathbb{R}}^n\to {\mathbb{R}}^l$

How to interpret this? Think of any vector $x\in {\mathbb{R}}^n$. That vector is getting fed to a linear function $f(\cdot )$ and produces a vector in ${\mathbb{R}}^m$. This is equivalent to multiplying the vector with $\mathbf{B}\in {\mathbb{R}}^{m\times n}$. The resultant vector in ${\mathbb{R}}^m$ gets fed to another linear function $g(\cdot )$ which transforms the vector into a vector in ${\mathbb{R}}^l$. This is equivalent to multiplying the vector by matrix $\mathbf{A}\in {\mathbb{R}}^{l\times m}$. A visualization is given below:

Composing Transformations §

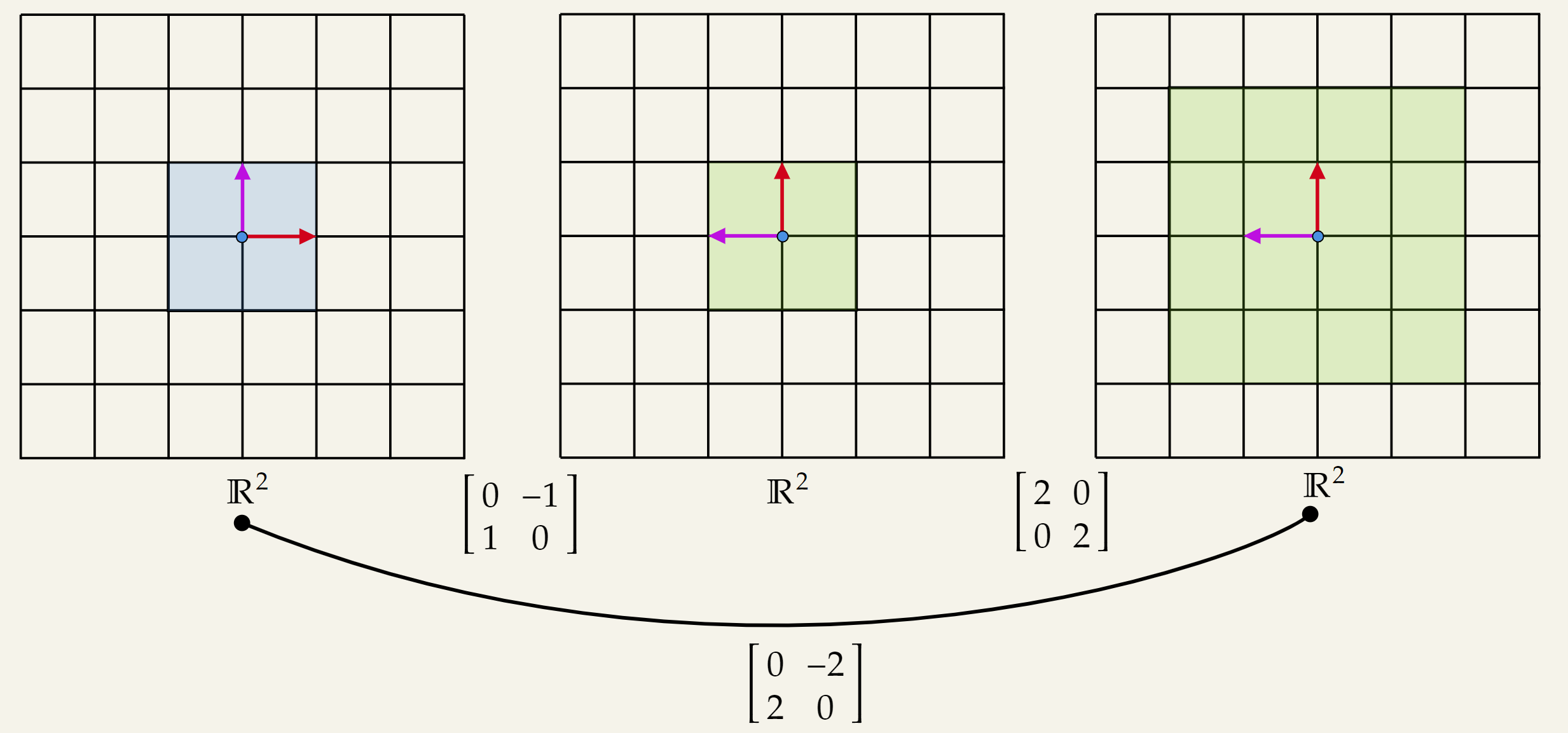
A better way to interpret matrix matrix multiplication is as composing transformations. In Matrix Multiplication as Transformation some “elementary” transformation was mentioned. We can compose those transformations to create more complex transformations. Sometimes it is better to think about it the other way meaning decomposing a complex transformation into smaller “elementary” transformations.

Consider the following matrix matrix transformation;

$$\left[\begin{array}{ll}2& 0\\ 0& 2\end{array}\right]\times \left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}0& -2\\ 2& 0\end{array}\right]$$

Here, two separate types of transformation is getting composed which are rotation followed by a uniform stretching.

Formula for finding each element of a Matrix Matrix multiplication §

$\mathbf{A}\in {\mathbb{C}}^{l\times m}$, $\mathbf{B}\in {\mathbb{C}}^{m\times n}$ and $\mathbf{C}\in {\mathbb{C}}^{l\times n}$ .

$$\mathbf{AB}=\left[\begin{array}{ccc}-& {\mathbf{a}}_1^{{\prime }^{\top }}& -\\ -& {\mathbf{a}}_2^{{\prime }^{\top }}& -\\ & ⋮& \\ -& {\mathbf{a}}_l^{{\prime }^{\top }}& -\end{array}\right]\left[\begin{array}{cccc}\mid & \mid & & \mid \\ {\mathbf{b}}_1& {\mathbf{b}}_2& \dots & {\mathbf{b}}_n\\ \mid & \mid & & \mid \end{array}\right]$$

Expanding this out will give the following expression:

$$\left[\begin{array}{cccc}{\mathbf{a}}_1^{{\prime }^{\top }}{\mathbf{b}}_1& {\mathbf{a}}_1^{{\prime }^{\top }}{\mathbf{b}}_2& \cdots & {\mathbf{a}}_1^{{\prime }^{\top }}{\mathbf{b}}_n\\ {\mathbf{a}}_2^{{\prime }^{\top }}{\mathbf{b}}_1& {\mathbf{a}}_2^{{\prime }^{\top }}{\mathbf{b}}_2& \cdots & {\mathbf{a}}_2^{{\prime }^{\top }}{\mathbf{b}}_n\\ ⋮& ⋮& \ddots & ⋮\\ {\mathbf{a}}_l^{{\prime }^{\top }}{\mathbf{b}}_1& {\mathbf{a}}_l^{{\prime }^{\top }}{\mathbf{b}}_2& \cdots & {\mathbf{a}}_l^{{\prime }^{\top }}{\mathbf{b}}_n\end{array}\right]$$

Each element in the result matrix is just an inner product. This makes writing out the general form really easy. If we want to access the element from the $i^{\text{th}}$ row and $j^{\text{th}}$ column, we can apply the following formula:

$${\mathbf{C}}_{ij}=(\mathbf{AB}{)}_{ij}={\mathbf{a}}_i^{{\prime }^{\top }}{\mathbf{b}}_j=\sum _{k=1}^m{a}_{ik}{b}_{kj}$$

Note that, we are summing over $m$ number of elements because both ${\mathbf{a}}_i^{{\prime }^{\top }}$ and ${\mathbf{b}}_j$ has a length of $m$.

References §

1. Margalit, Dan, and Joseph Rabinoff. “Matrix Multiplication.” Interactive Linear Algebra, textbooks.math.gatech.edu/ila/matrix-multiplication.html.