In this section, I will go through different types of matrices and visualize what transformation happens when we apply that matrix to vectors.
Considerations
- Obviously, these transformations can be generalized to any vector space of . But for the ease of visualization I will keep it limited to .
- In addition, based on the discussion in Matrix Vector Multiplication and Linearity it is pretty obvious, understanding how the basis vectors transforms is all we require to get a intuition about the transformation.
- Hence, I will illustrate all the vectors within one unit distance from the origin with a colored rectangle.
Other Online Interactive Tools to visualize:
I think playing with these tools is the best way to appreciate matrices as transformations.
Caution about terminology
Note that some of the terminology used in this page is not standarized. Word like “Stretching” or “Scaling” can be interpreted in different ways and sometimes you might need to perform some mental gymnastics to adapt.
Identity matrix
By definition, identity matrix is a square matrix with along the diagonals. When we apply the identity matrix to any vector in , nothing actually happens and all the vectors stay where it was originally.
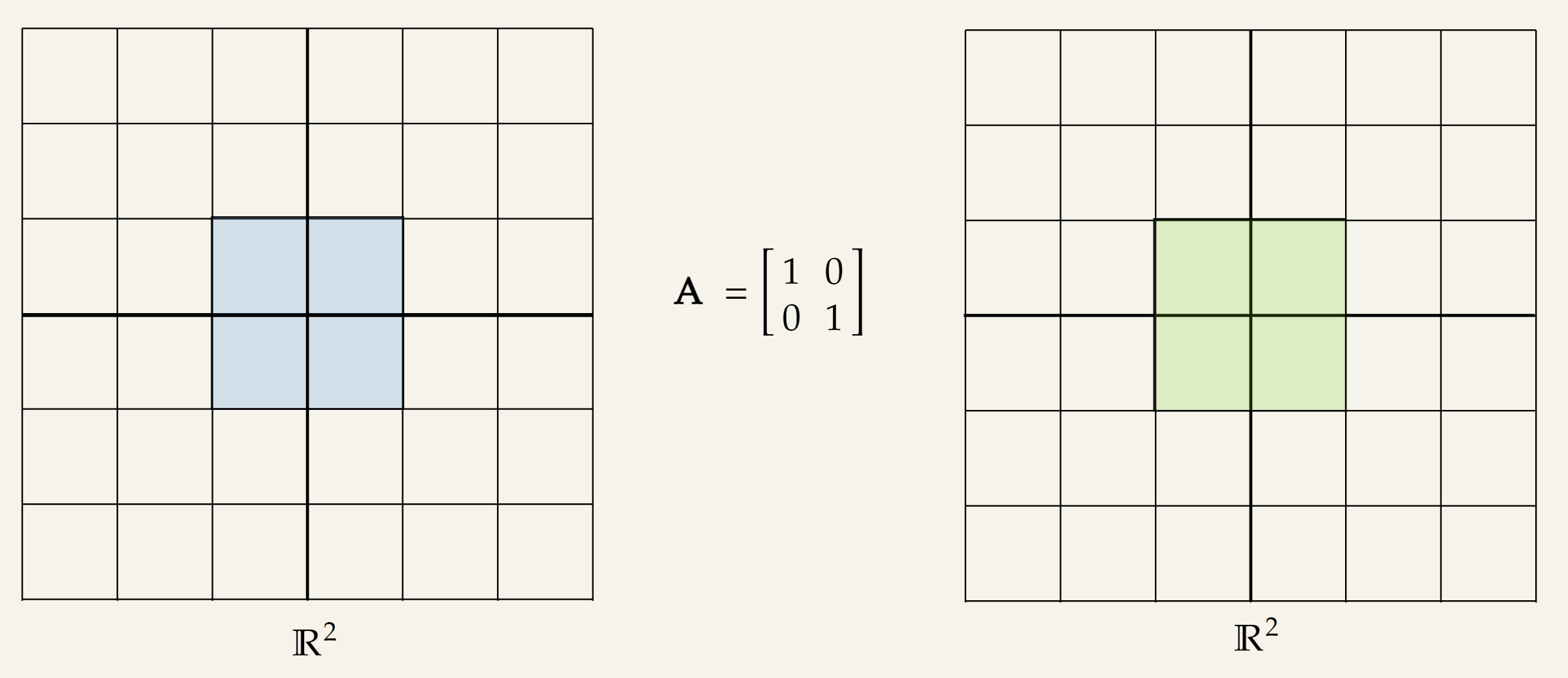
The reason behind that is that every column of the identity matrix is a standard basis vector.
Diagonal matrices | Scaling Transformations
A diagonal matrix has non-zero diagonal elements (). All the off-diagonal elements are zero (). And, by definition, we will consider it a square matrix.
▪ Uniform Stretching Transformation
Consider the following :
Visually, it will look like the following:
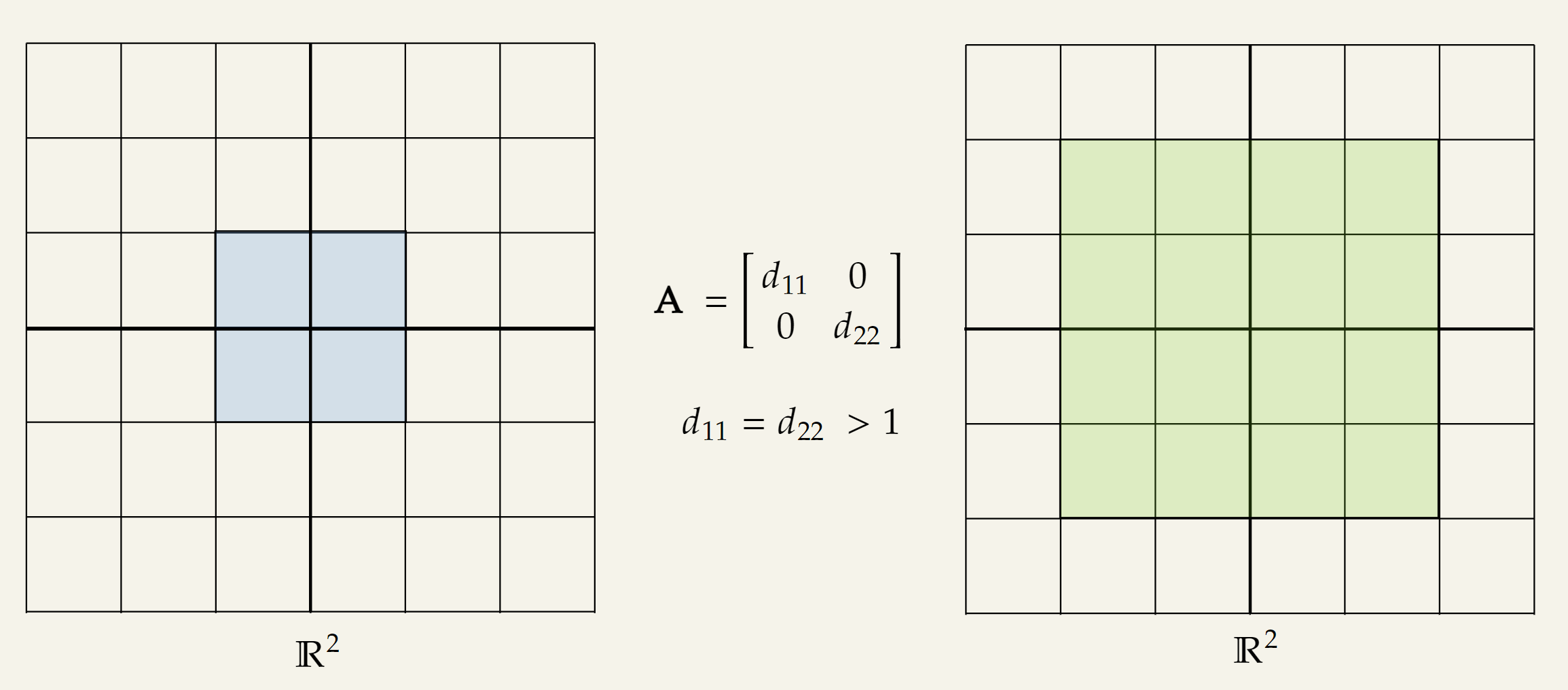 The geometric interpretation of this transformation is:
The geometric interpretation of this transformation is:
- An uniform stretching along both axis.
- It performs the same amount of “stretch” along both axis because .
- It is a “stretching” transformation because .
- The exact value of will determine the “amount of stretch”.
As an example consider the following matrix :
▪ Non-Uniform Stretching Transformation
Visually, it will look like the following two diagrams:
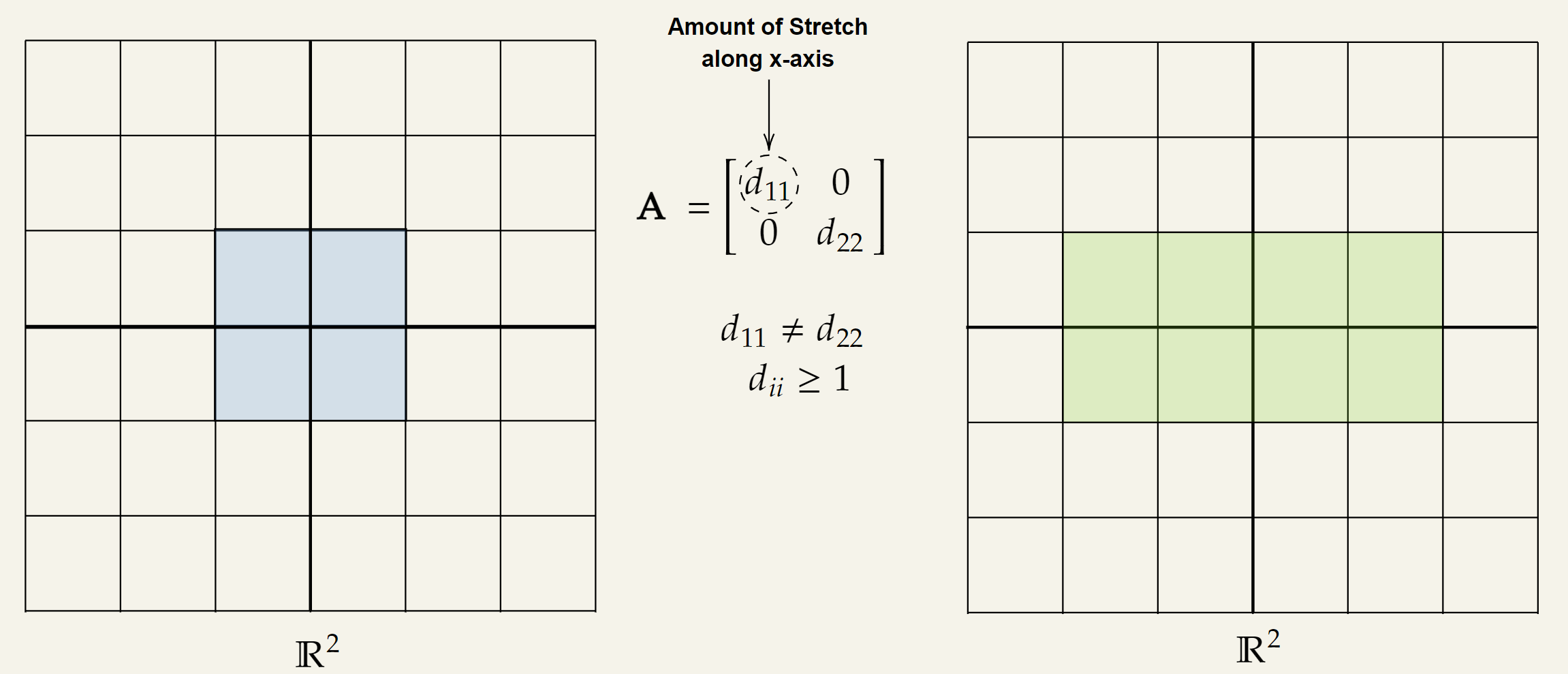 As an example consider the following matrix :
As an example consider the following matrix :
Here, the vectors will get stretched by a factor of along the and will stay constant along the .
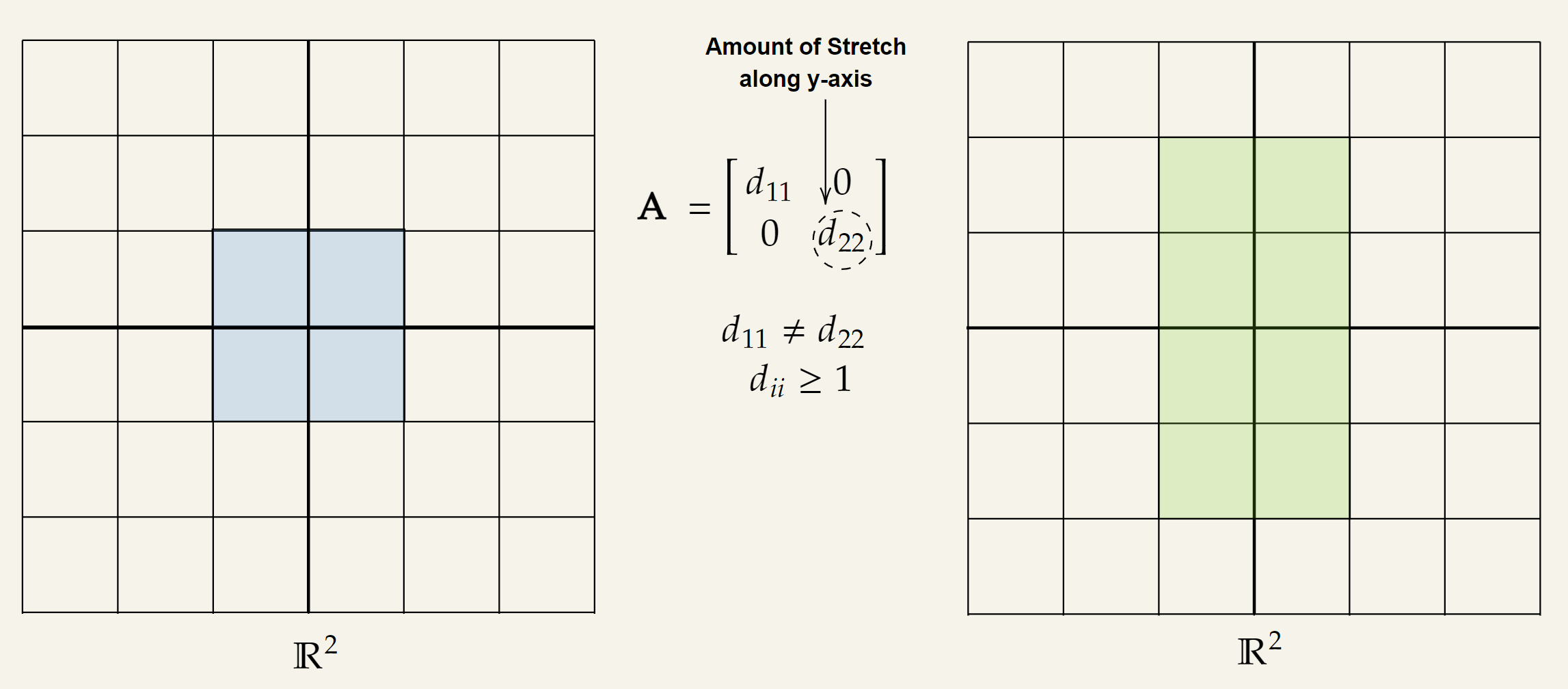
As an example consider the following matrix :
Here, the vectors will get stretched by a factor of along the and will stay constant along the .
The geometric interpretation of this transformation is:
- An non-uniform stretching which is determined by the value of .
- It is a “stretching” transformation because .
- If both diagonal entries are equal to (violating ), then it transforms to an identity matrix.
The reason behind keeping one diagonal elements fixed at 1 is the ease of visualization.
▪ Uniform Shrinking Transformation
Consider the following :
Visually, it will look like the following:
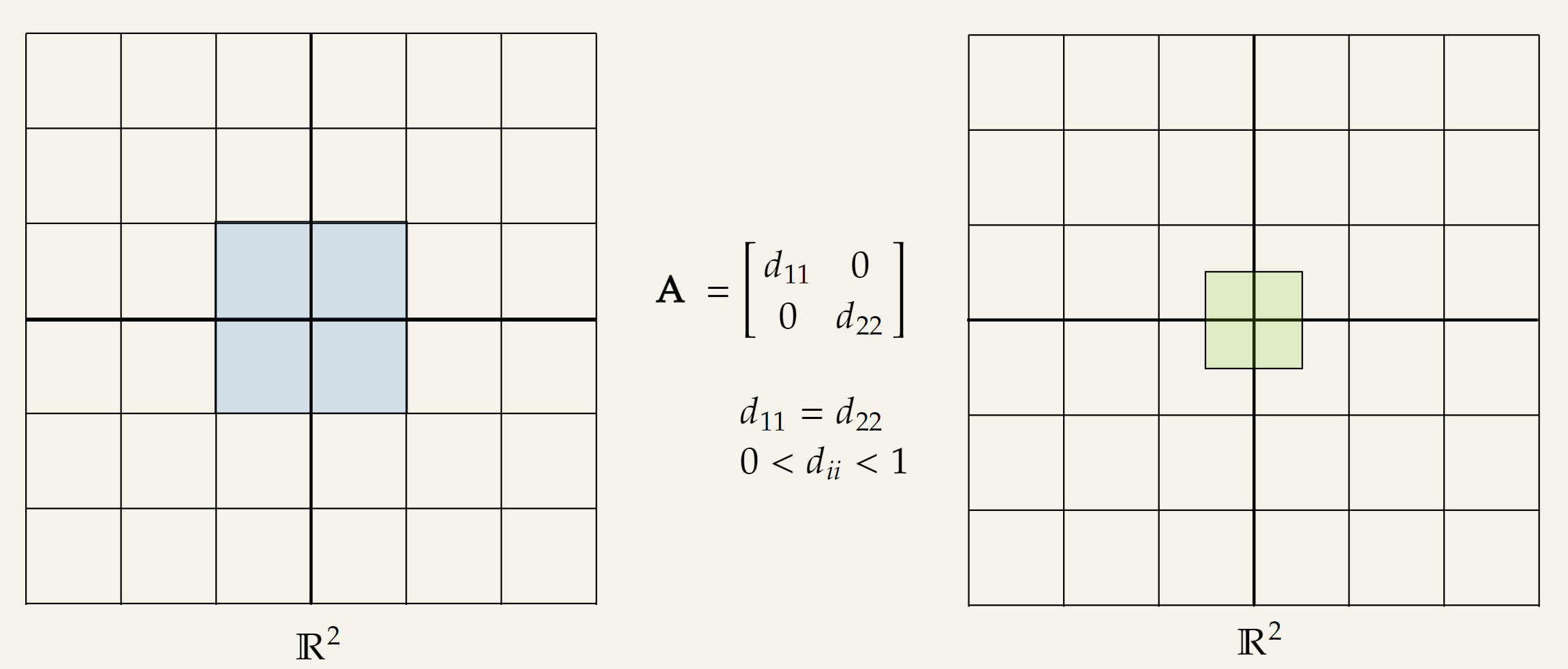 The geometric interpretation of this transformation is:
The geometric interpretation of this transformation is:
- An uniform shrinking along both axis.
- It performs the same amount of “shrinkage” along both axis because .
- It is a “shrinking” transformation because .
- The exact value of will determine the amount of shrinkage.
▪ Non-Uniform Shrinking Transformation
Visually it will look like the following two diagrams:
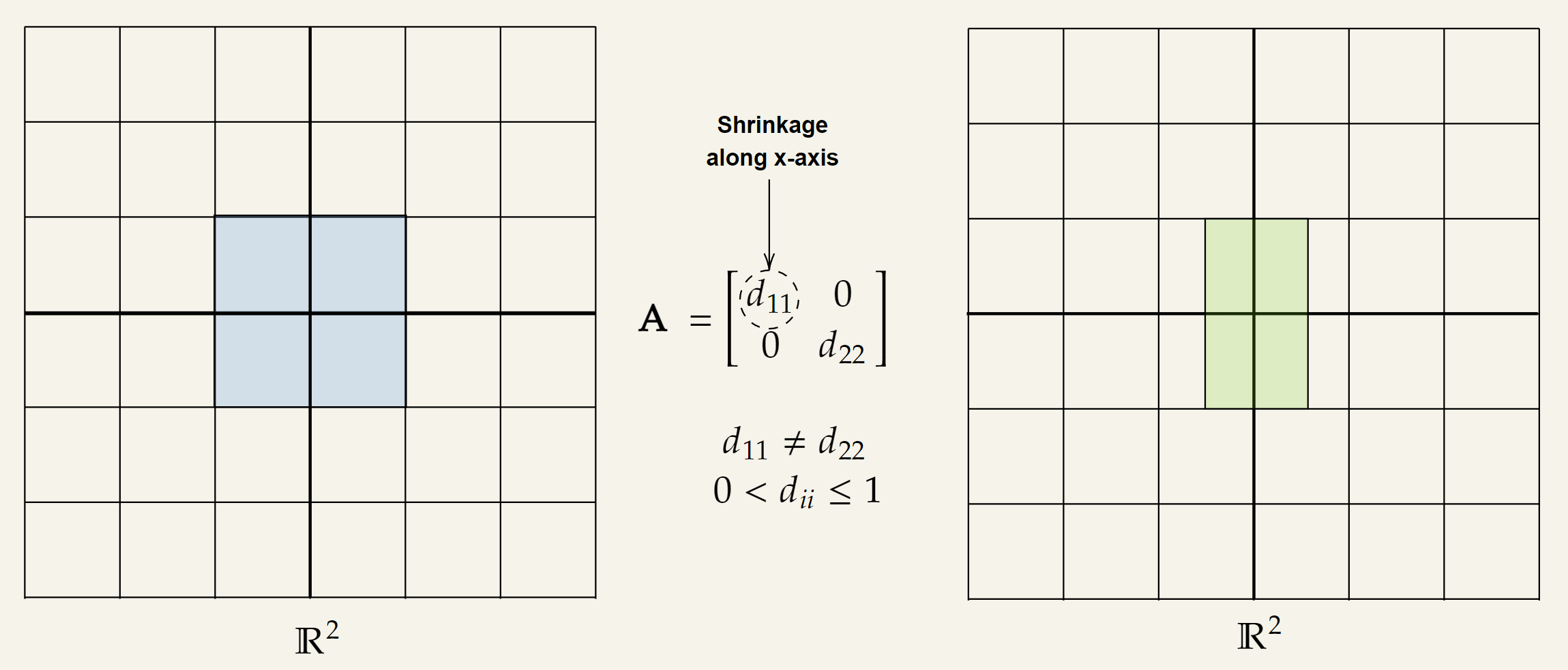
As an example consider the following matrix :
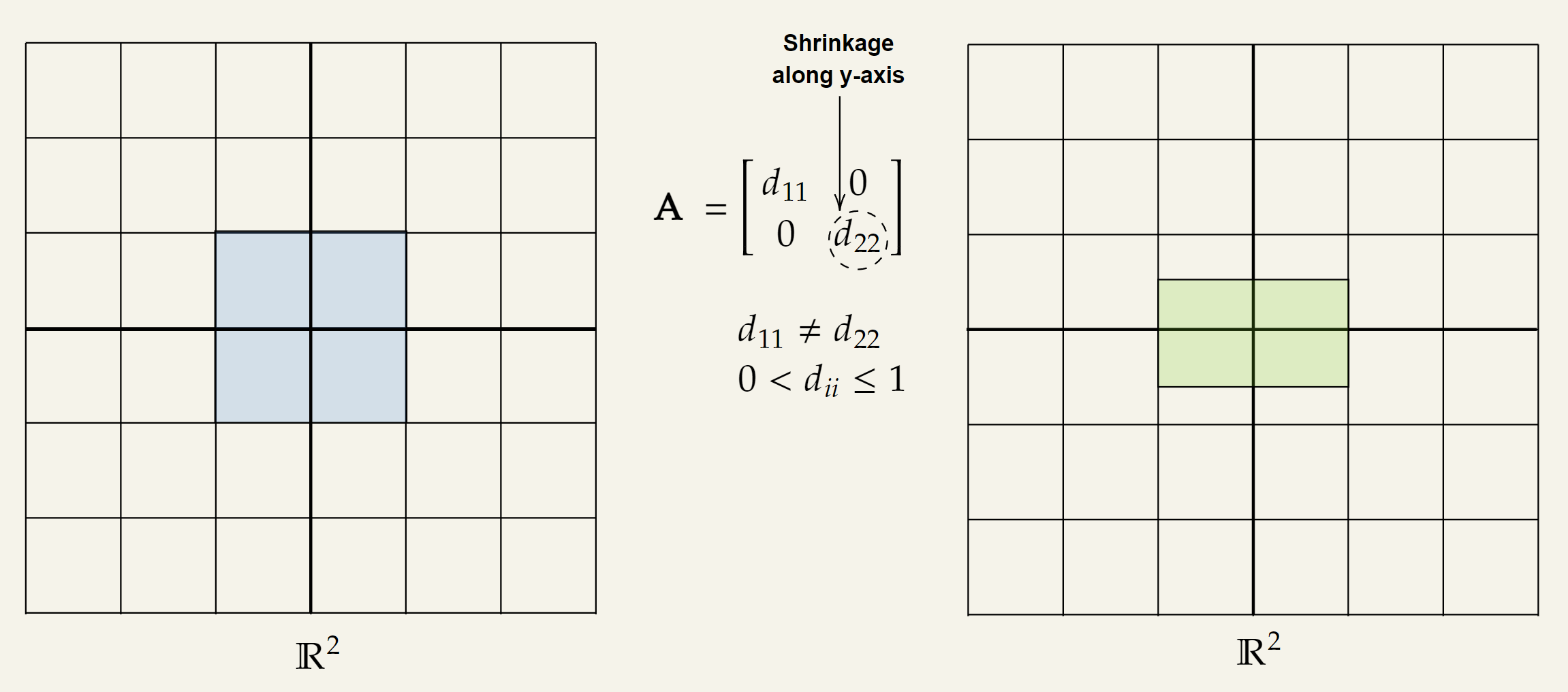
As an example consider the following matrix :
The geometric interpretation of this transformation is:
- An non-uniform shrinking determined by .
- It is a shrinking transformation because
The reason behind keeping one diagonal elements fixed at 1 is the ease of visualization.
Diagonal matrices | Reflection Transformations
To visualize these transformations we need to take into account the orientation of vectors. In addition, to visualize pure reflection without any scaling the absolute value of the diagonal elements need to be .
Reflection along the y-axis:
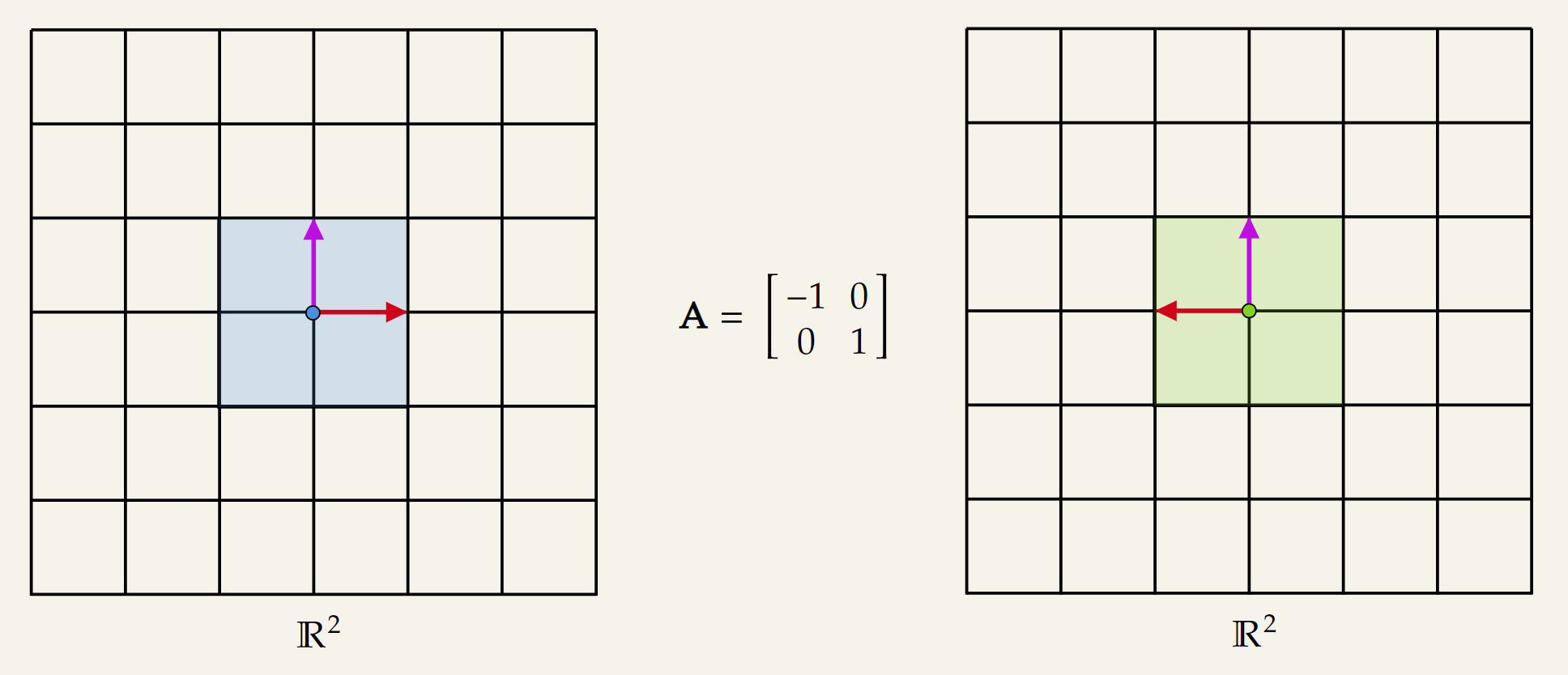
Reflection along the x-axis:
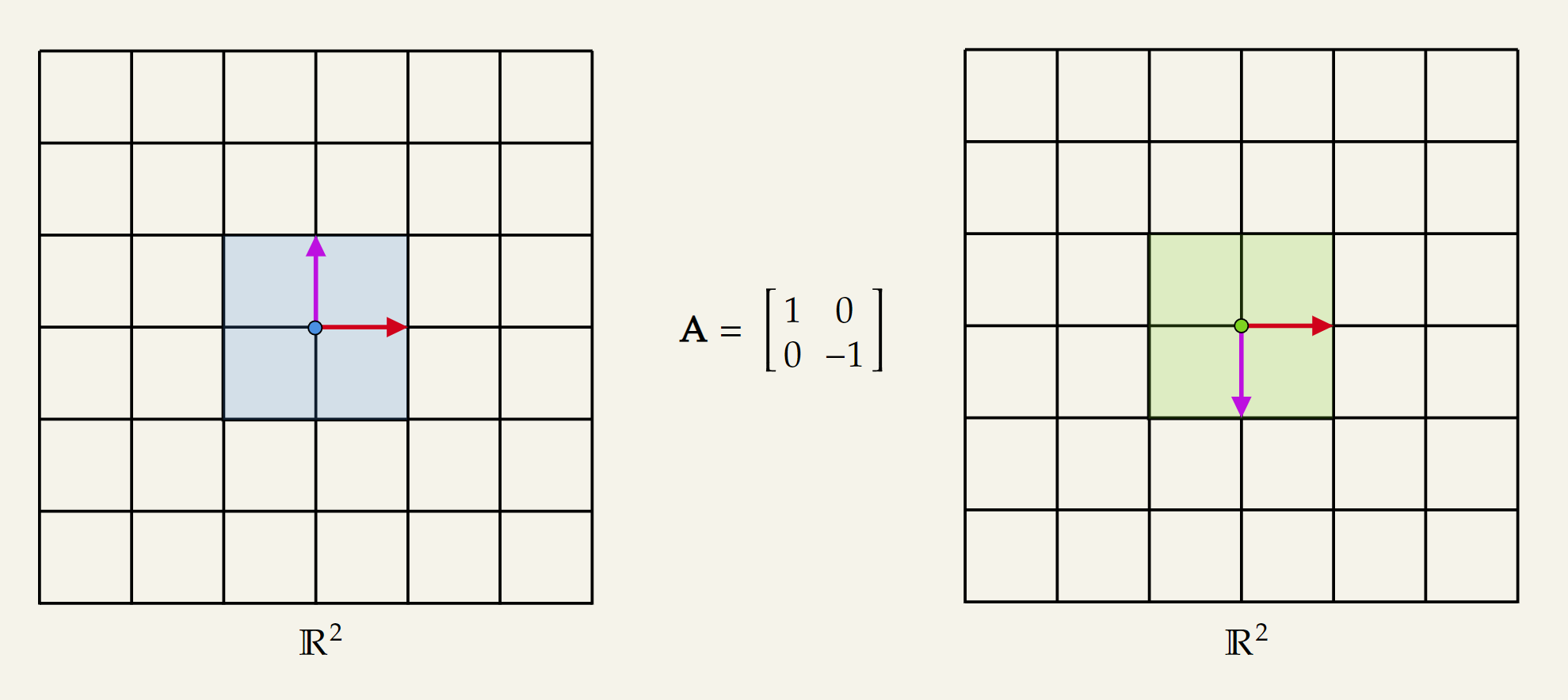
Reflection along both the x and y-axis:
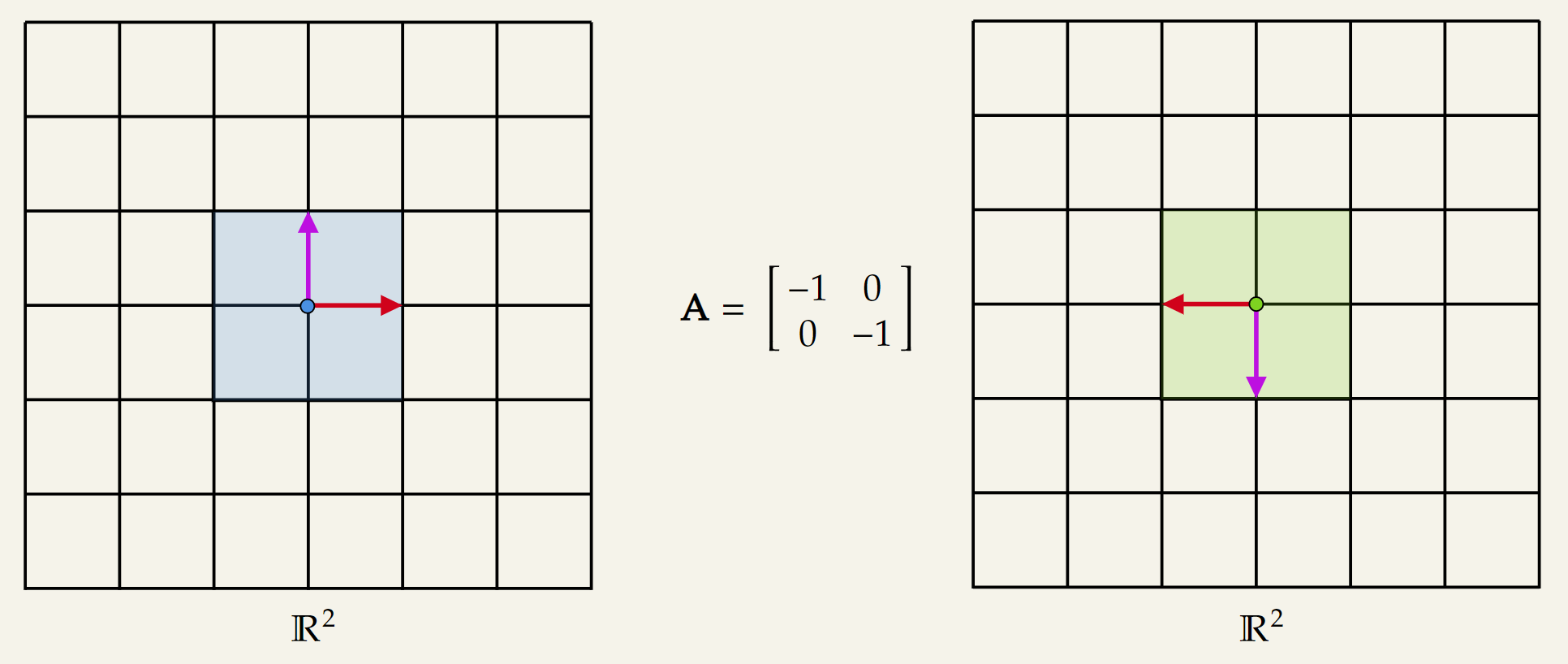
These reflection transformations can not be achieved through rotations.
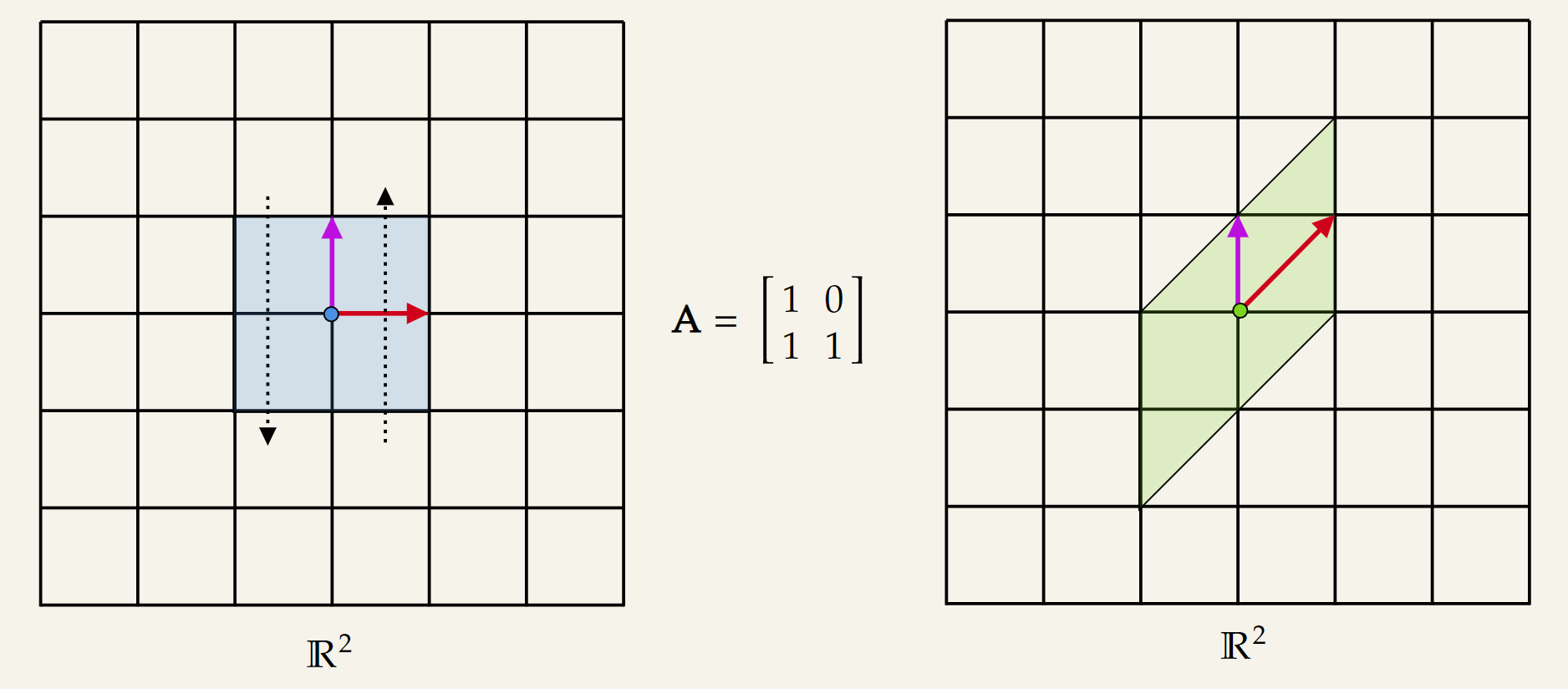
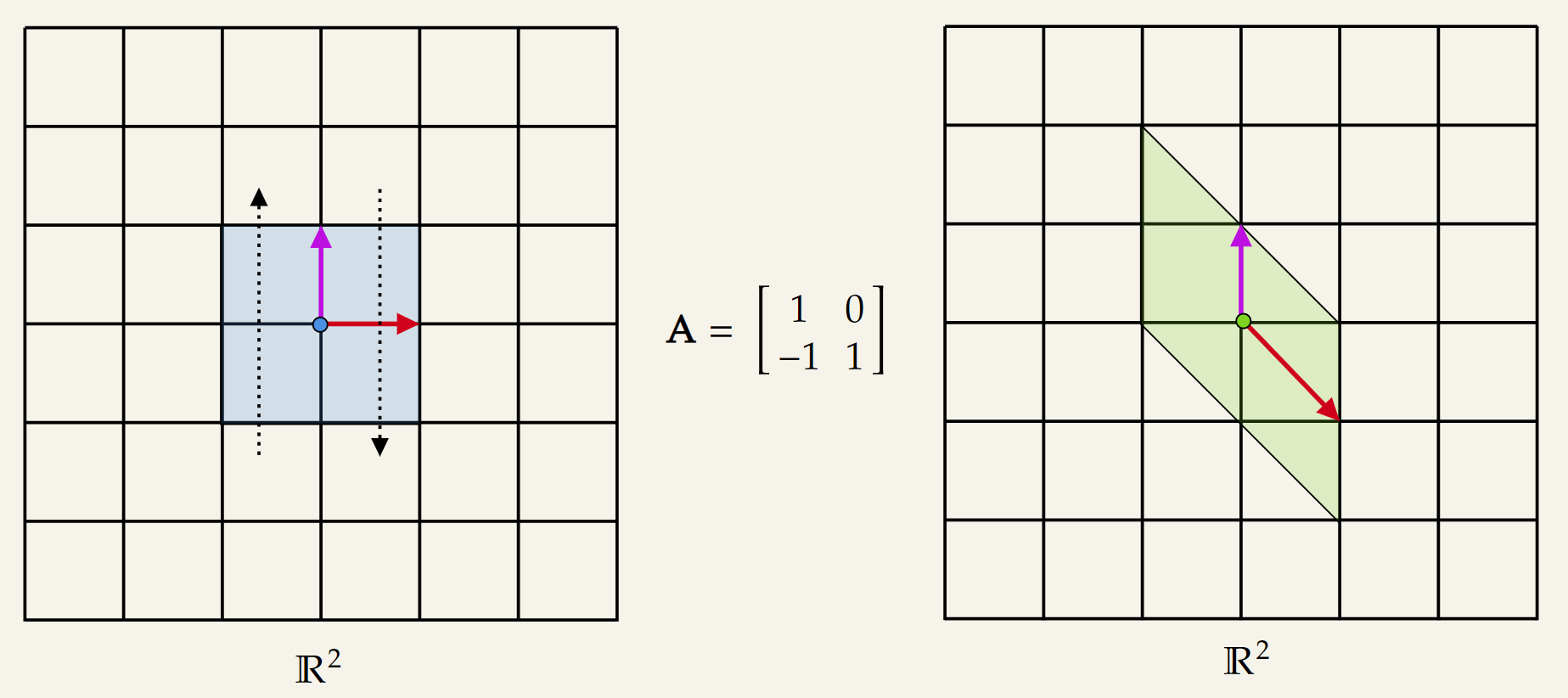
Shear Transformation
For shearing transformation, the off-diagonal terms need to be modified. For ease of visualization, I kept the off-diagonal element to either or .
Shearing parallel to the x-axis:
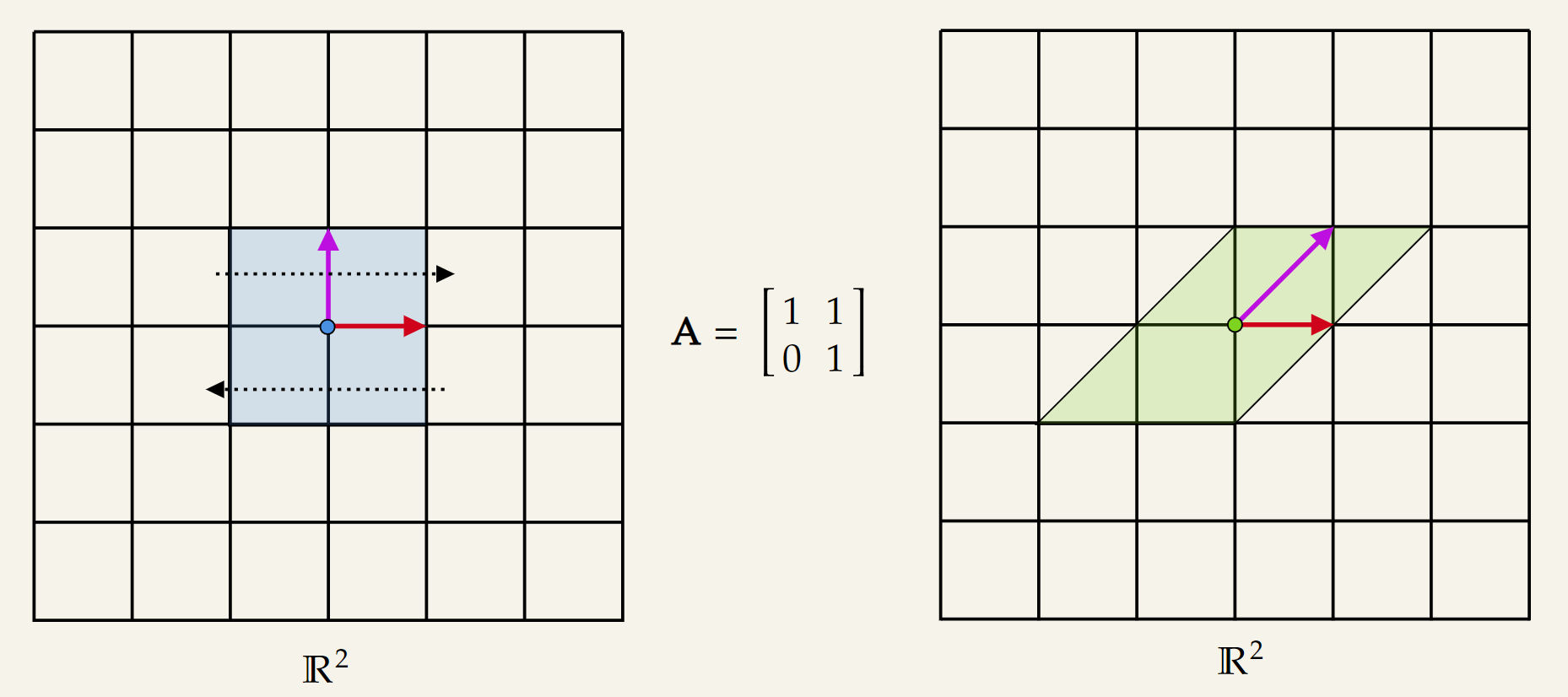
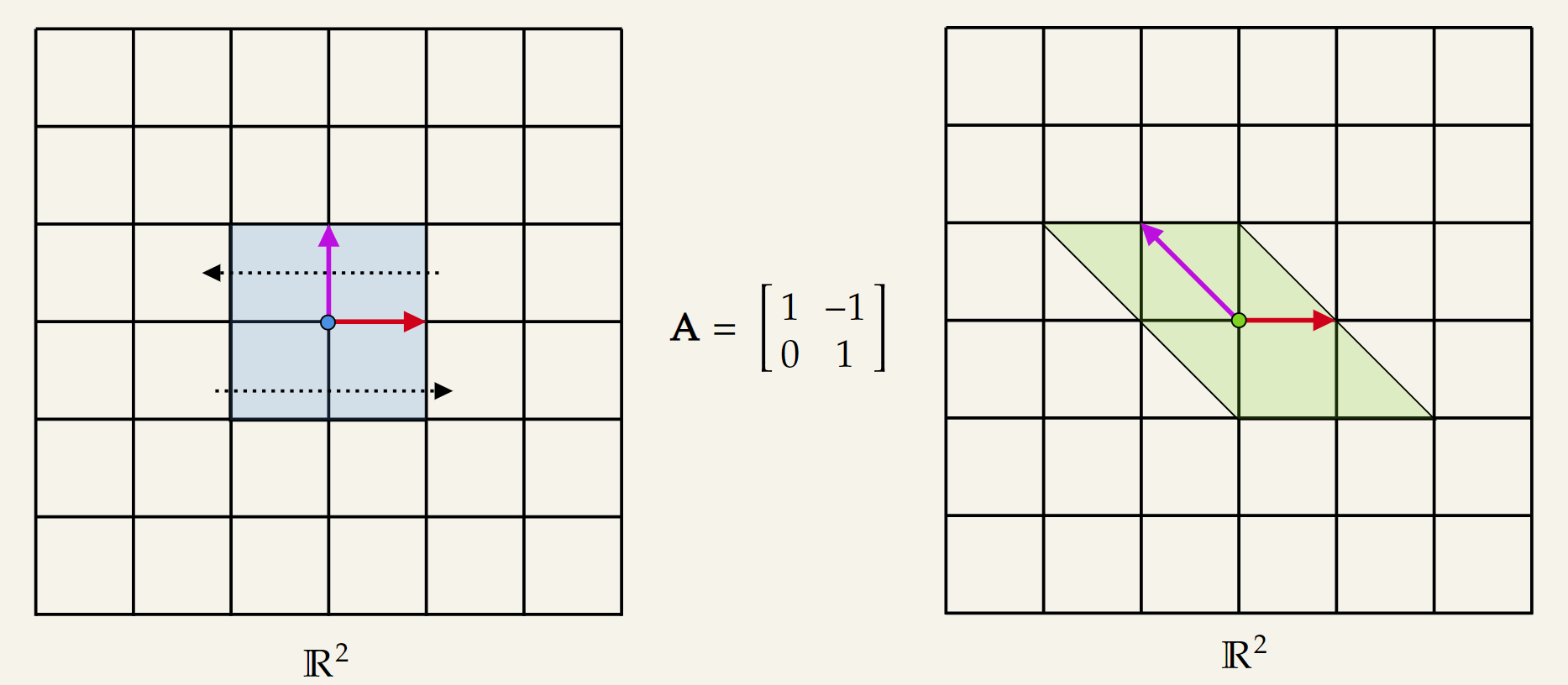
Shearing parallel to the y-axis:
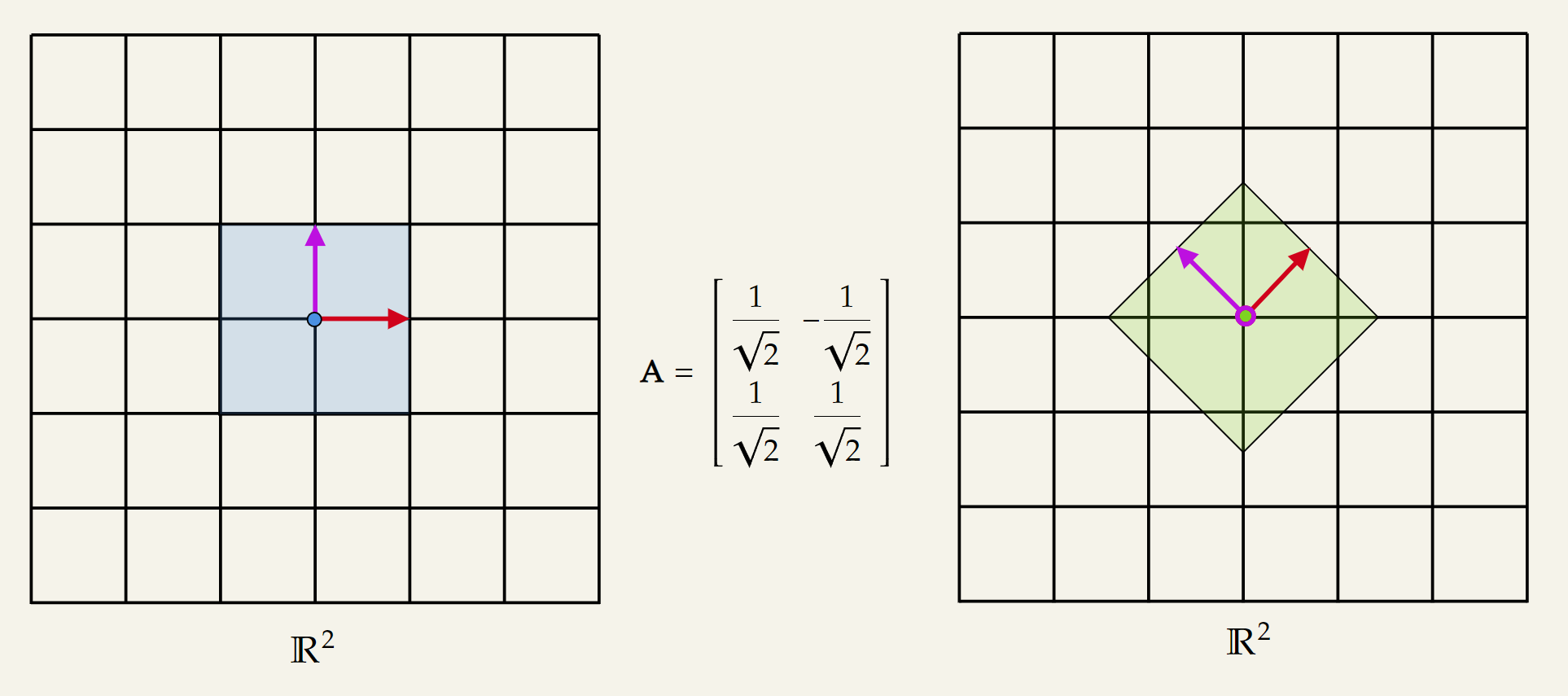
Orthogonal Matrices | Rotational Transformation
Orthogonal Matrices only perform rotation transformation to vectors without any scaling. There is an extensive explanation for this type of matrix in the later sections, hence, I will just provide one simple example of an orthogonal matrix.
By varying the value of , we can generate orthogonal matrices which provide amount of rotations. If is set to , we get the following matrix:
Let’s see another example, where the matrix performs a rotation.
References
- Kernel, Visual. Visualize Different Matrices Part1 | SEE Matrix, Chapter 1. 14 Mar. 2022, youtu.be/7Gtxd-ew4lk.
- Gundersen, Gregory. A Geometrical Understanding of Matrices. 24 Oct. 2018, gregorygundersen.com/blog/2018/10/24/matrices/.