1.10. Kernel and Null Space

Let’s start with the definition, Consider a matrix $\mathbf{A}\in {\mathbb{R}}^{m\times n}$

$$\ker (\mathbf{A}):=\left\{x\in {\mathbb{R}}^n\mid \mathbf{Ax}=0\right\}\subseteq {\mathbb{R}}^n$$

Interpretation:

• All the vectors $\mathbf{x}\in {\mathbb{R}}^n$ are going through the transformation $\mathbf{Ax}$.
• A set of vectors $\mathbf{x}\in {\mathbb{R}}^n$ is getting mapped to $0$ after the transformation.

Let’s visualize this with an image :

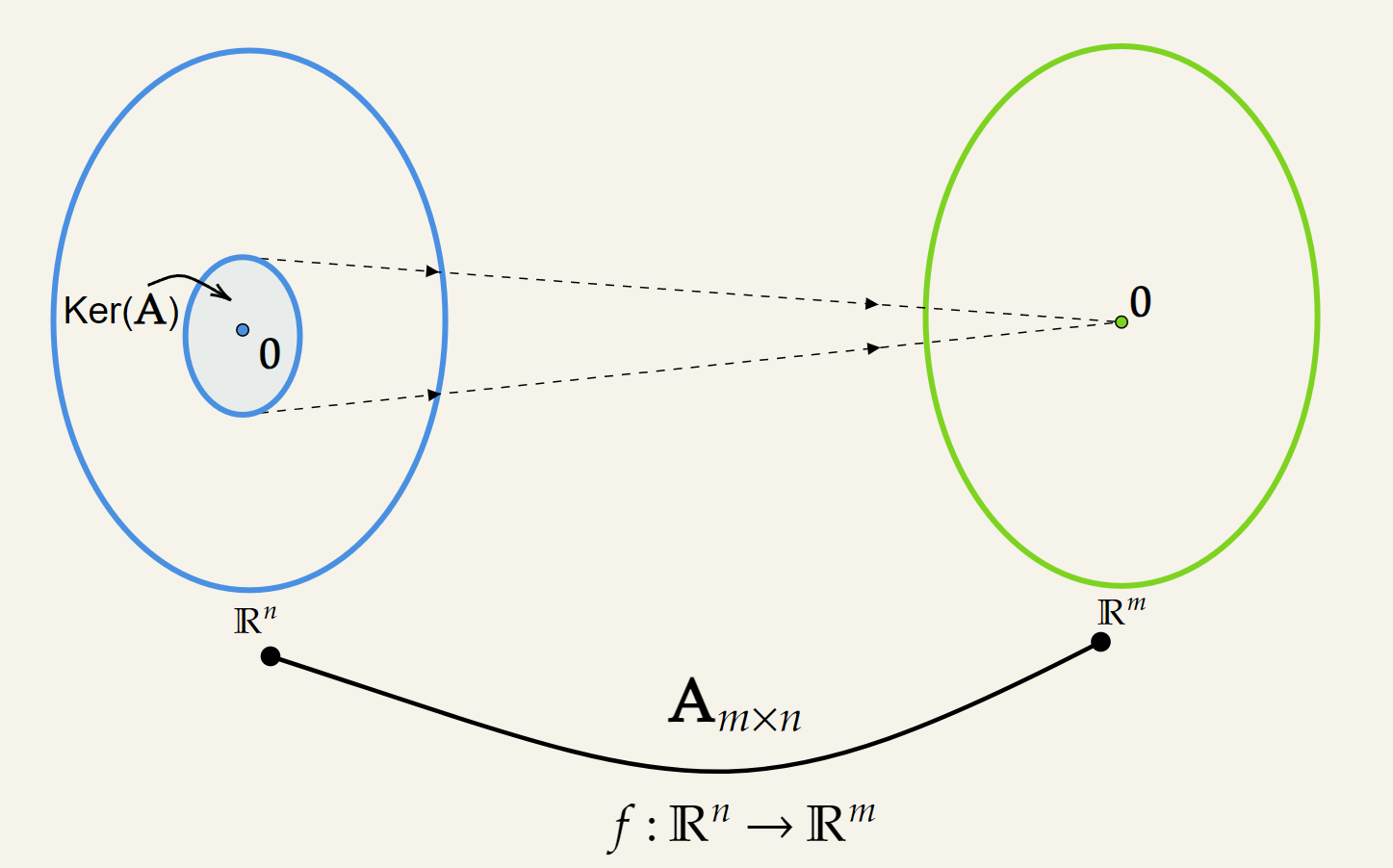
We can see that the zero vector is always going to be included in the Kernel. This is obvious, because if in the transformation $\mathbf{Ax}$ , the vector $\mathbf{x}$ is $0$, the resultant value is $0$.

Connecting to Null Space §

The kernel of a matrix $\mathbf{A}\in {\mathbb{R}}^{m\times n}$ forms a subspace in ${\mathbb{R}}^n$. The subspace is known as the null space of $\mathbf{A}$.

As the $0$ vector is always included in the null space, we say $0$ is the trivial null space. Any vector other than $0$ is referred to as the vectors in non-trivial null space.

Connecting to Solution of Homogenous Equations §

We can represent homogenous equations in matrix vector form as below :

$$\mathbf{Ax}=0$$

If $\mathbf{x}$ is in the null space of $\mathbf{A}$ that would mean, it satisfies the equations. This means the solution to the homogenous system of equation represented by $\mathbf{Ax}=0$ a subspace of ${\mathbb{R}}^n$ (null space to be exact).

The following can be thought of equivalent: $\mathrm{Ker}(\mathbf{A})\equiv \mathrm{Null}(\mathbf{A})$