1.13. Union and Intersection of Subspaces

Union of subspaces §

$$\boxed{\text{Union of two subspaces is not a subspace}}$$

Mathematically, if $W$ and $U$ are two subspaces then $W\cup U$ is not a valid subspace.

To get a concrete example, let’s restrict ourselves to ${\mathbb{R}}^2$ an consider two subspaces $W$ and $U$. In ${\mathbb{R}}^2$ two subspaces are represented by two infinite lines going through the origin. 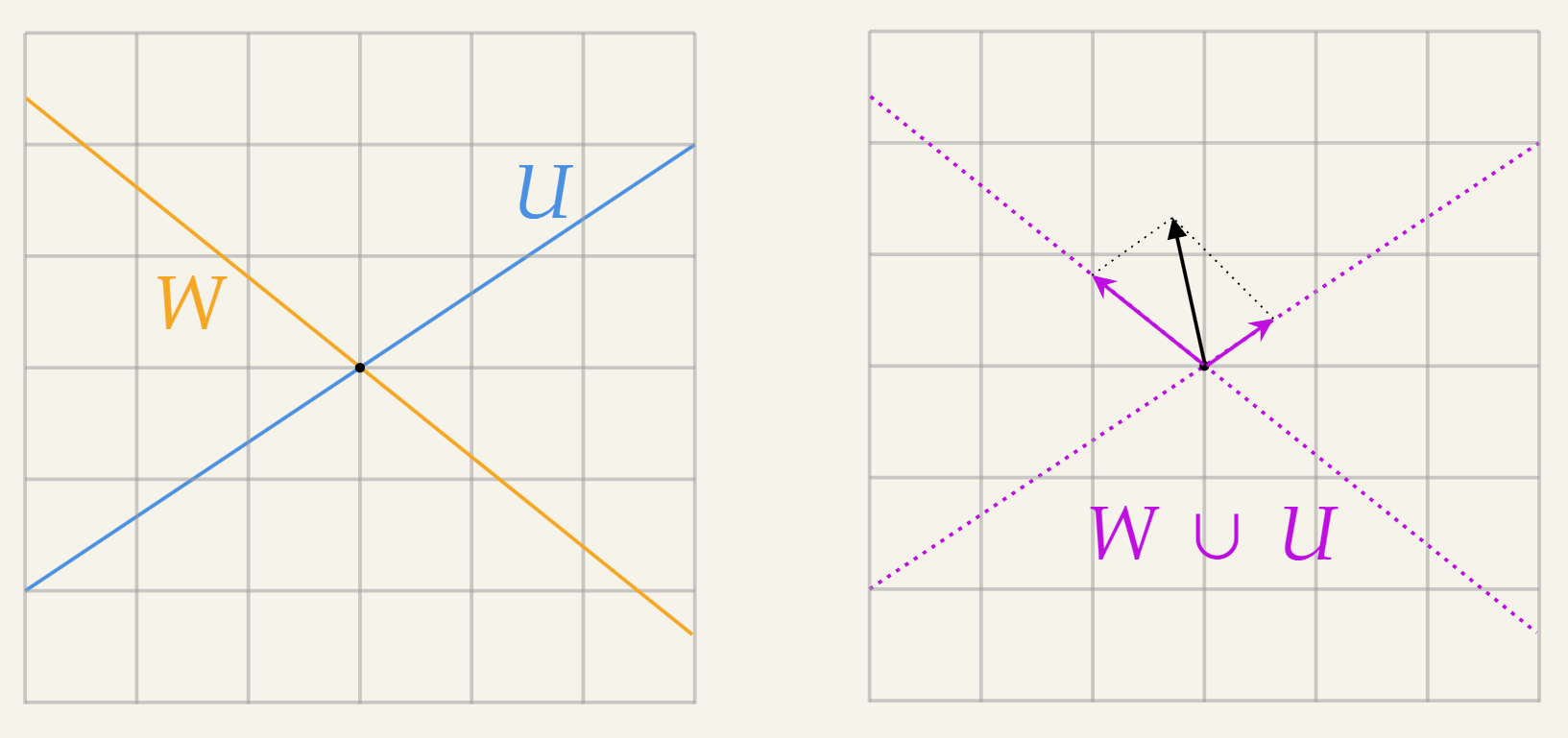Visually we can see of we take any two vector from $W$ and $U$, the summation of them is not contained in $W\cup U$.

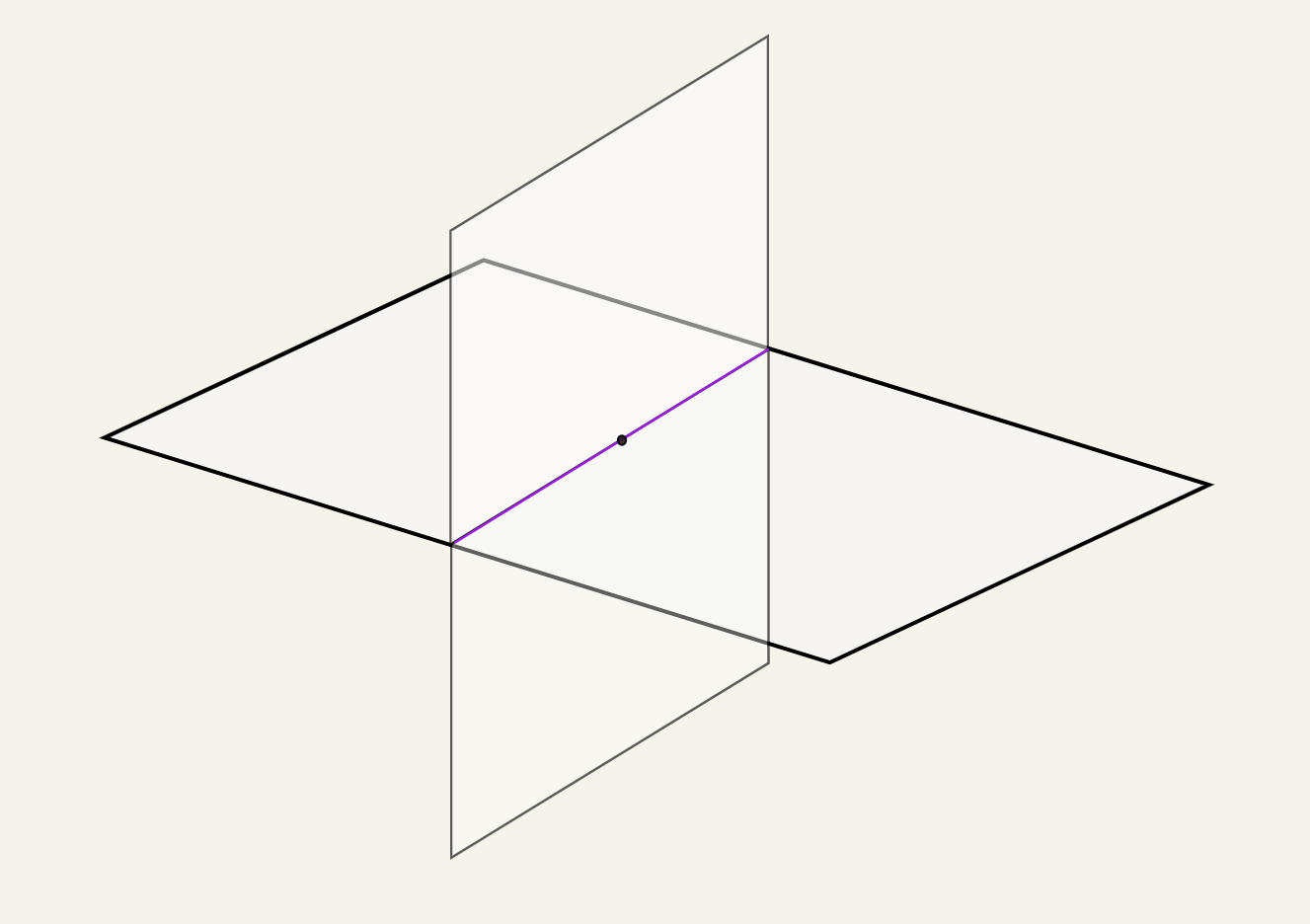
It also holds true in ${\mathbb{R}}^3$ where the two subspaces are two planes going through the origin.

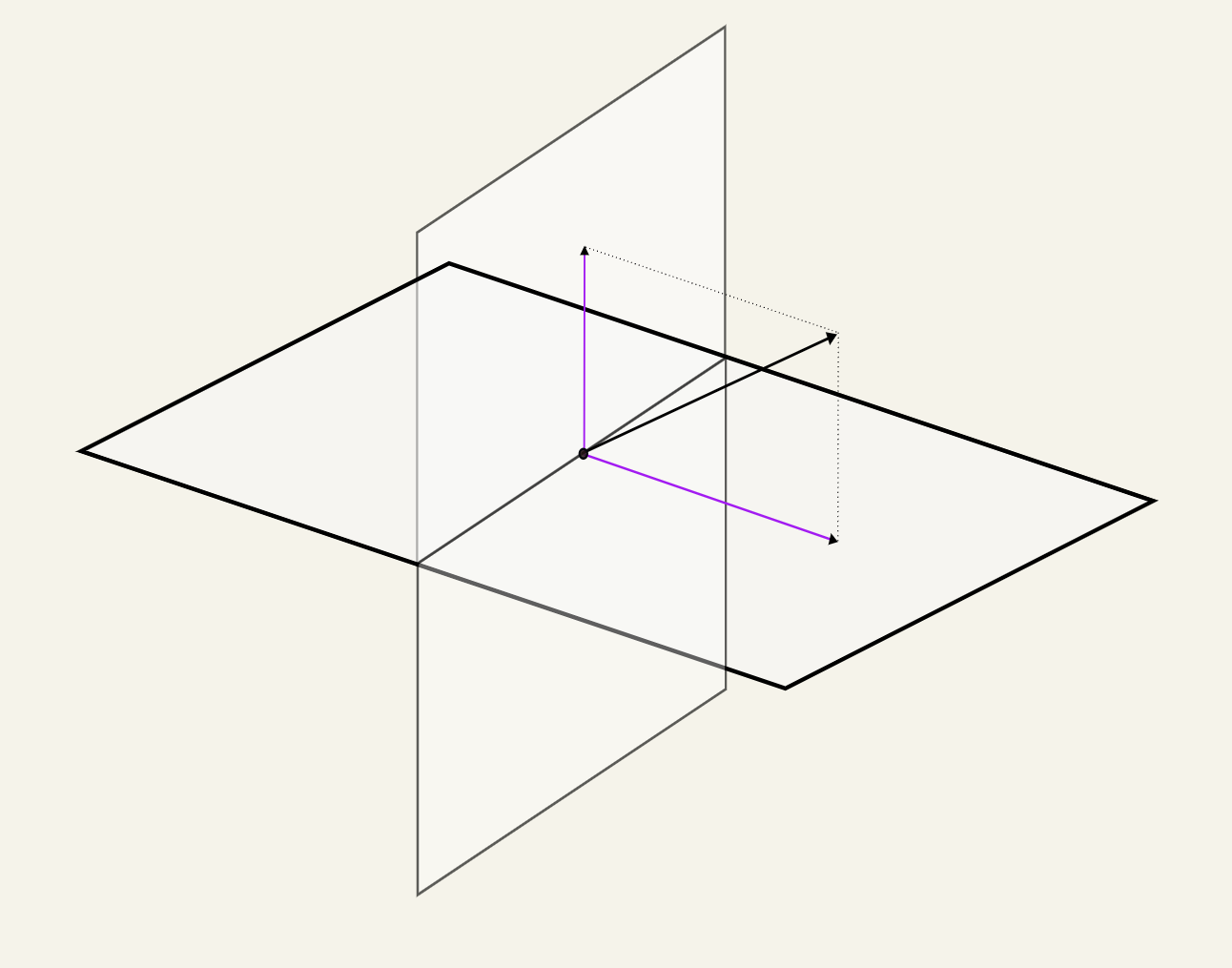
One important thing to mention here, $W\cup U$ does contain the zero vector and closed under scalar multiplication. The property that fails is addition operation.

Intersection of subspaces §

$$\boxed{\text{Intersection of two subspaces is a subspace}}$$

Mathematically, if $W$ and $U$ are two subspaces then $W\cap U$ is also a subspace.

To get a concrete example, let’s restrict ourselves to ${\mathbb{R}}^2$ an consider two subspaces $W$ and $U$. The intersection will only contain the zero vector. We know that $0$ is subspace.

In ${\mathbb{R}}^3$, the intersection is a line that goes through the origin which is subspace itself.