1.14 Direct Sum of Subspaces

Direct sum of two subspace (or vector space) $W$ and $U$ is denoted by $W\oplus U$.

Say, $V$ is the resultant subspace from the direct sum. To be a valid direct sum the following two properties need to hold:

• $V=W+U$ where $v\in V,w\in W,u\in U$

$$v=w+u$$

• $W\cap U=\{0\}$

Another interpretation of this definition is : $v=w+u$ can be uniquely written.

Consider two subspaces $W$ and $U$.

Here, the subspace $W$ contains vector of the form shown below:

$$\left[\begin{array}{c}0\\ 0\\ c\end{array}\right]$$

And, the subspace $U$ contains vector of the form shown below:

$$\left[\begin{array}{c}a\\ b\\ 0\end{array}\right]$$

Visualization of direction sum is given below:

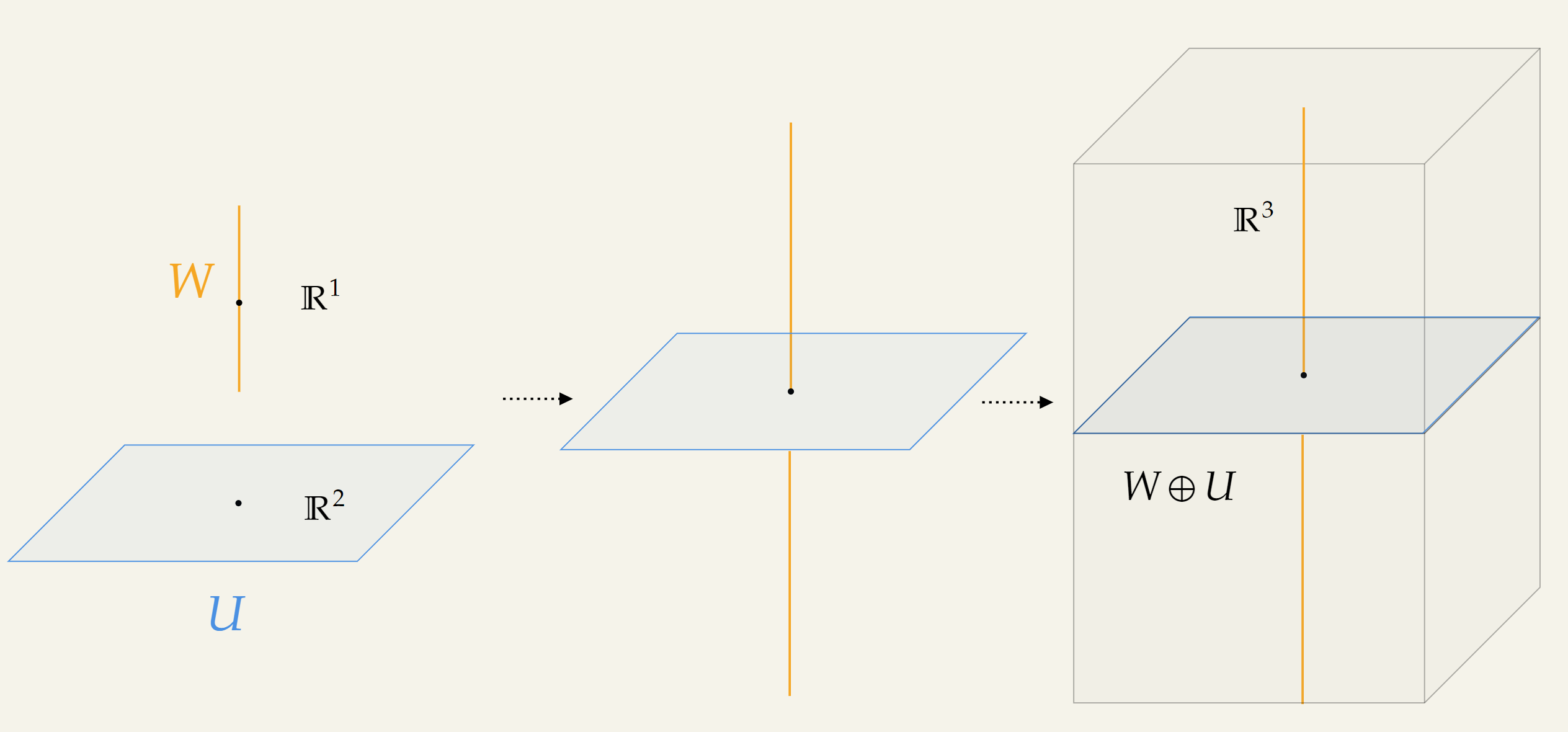We can clearly see that, when we add $w\in W$ and $u\in U$, there is only one way they can be added. And the resultant $v\in V$ will have the following form:

$$\left[\begin{array}{c}a\\ b\\ c\end{array}\right]$$

A counter example might provider better perspective. Consider the following:

$$v=w+u=\left[\begin{array}{c}0\\ d\\ c\end{array}\right]+\left[\begin{array}{c}a\\ b\\ 0\end{array}\right]=\left[\begin{array}{c}a\\ d+b\\ c\end{array}\right]$$

Here, the vector $v$ can be written in infinitely different ways as the value of $d$ and $b$ changes.