1.6. Span

Definition §

Let $S$ be a set of vectors in ${\mathbb{C}}^n$. The $\text{span}(S)$ is the set of vectors in ${\mathbb{C}}^n$ that are a linear combination of vectors in $S$.

This might sound a bit “formal” and hard to grasp. Just think of it this way; you are given a set of vectors from the vector space ${\mathbb{C}}^n$. Now from that set of vectors you can generate new vectors by taking linear combination of them. Now, by taking every possible linear combination you are going to get a resultant set of vectors. That resultant set of vectors is called the span of the original set of vectors you were given.

Formally, consider a set of vectors $S:=\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_n\}$

$$\begin{gathered} \mathrm{span}(S)=\left\{\sum _{\begin{array}{c}{\mathbf{v}}_i\in S\\ \\ {\alpha }_{i\in {\mathbb{C}}^n}\end{array} \\ }{\alpha }_i{\mathbf{v}}_i\right\} \end{gathered}$$

Visual Intuition of Span §

The idea of span is closely related to Linear independence. Let’s start with a single vector in ${\mathbb{R}}^2$ vector space.

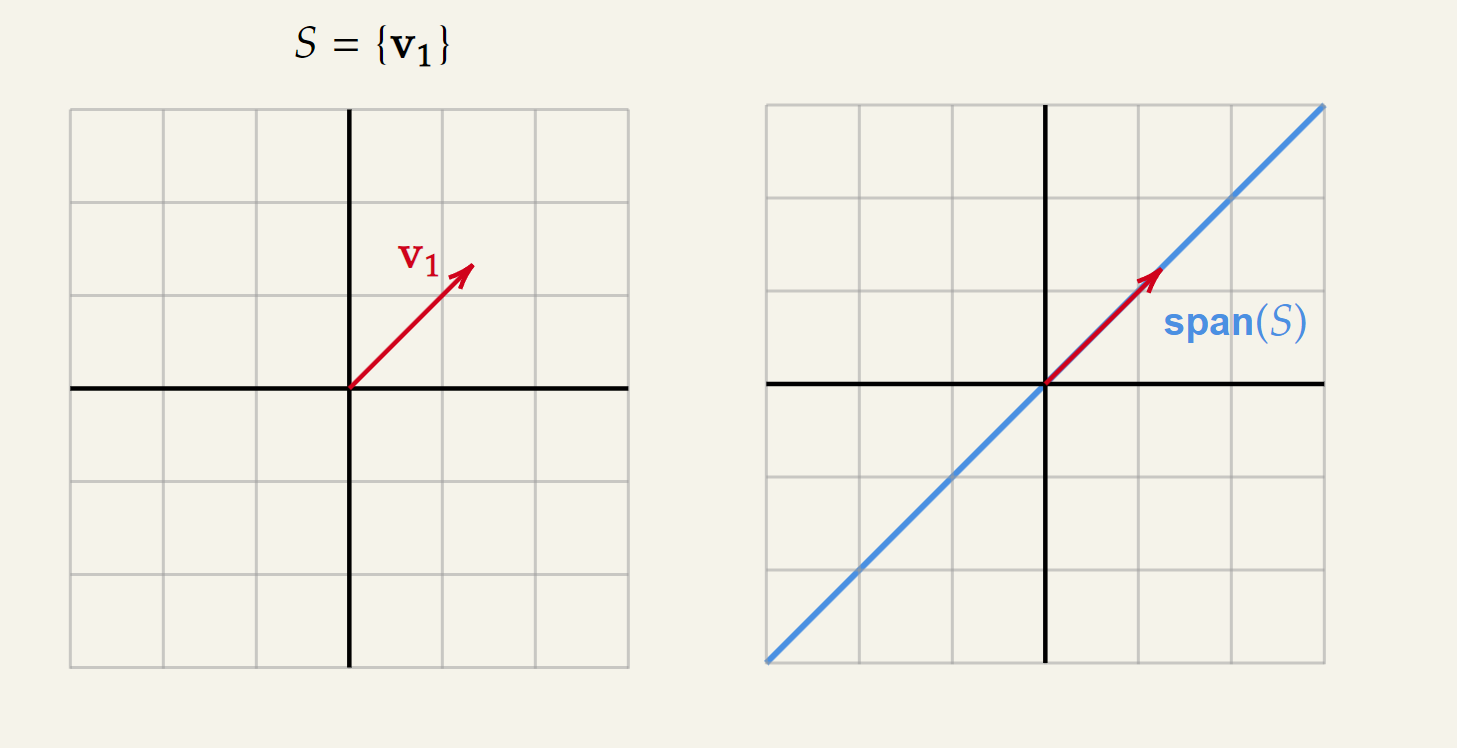
For a single vector $S=\{{\mathbf{v}}_1\}$, all we can do is perform scalar multiplication. This creates an infinite length line going through the origin which is $\text{span}(S)$

But if we consider any two vectors in ${\mathbb{R}}^2$ which are not parallel or in other words, not in the span of each other, the span of these two vectors is the entire plane.

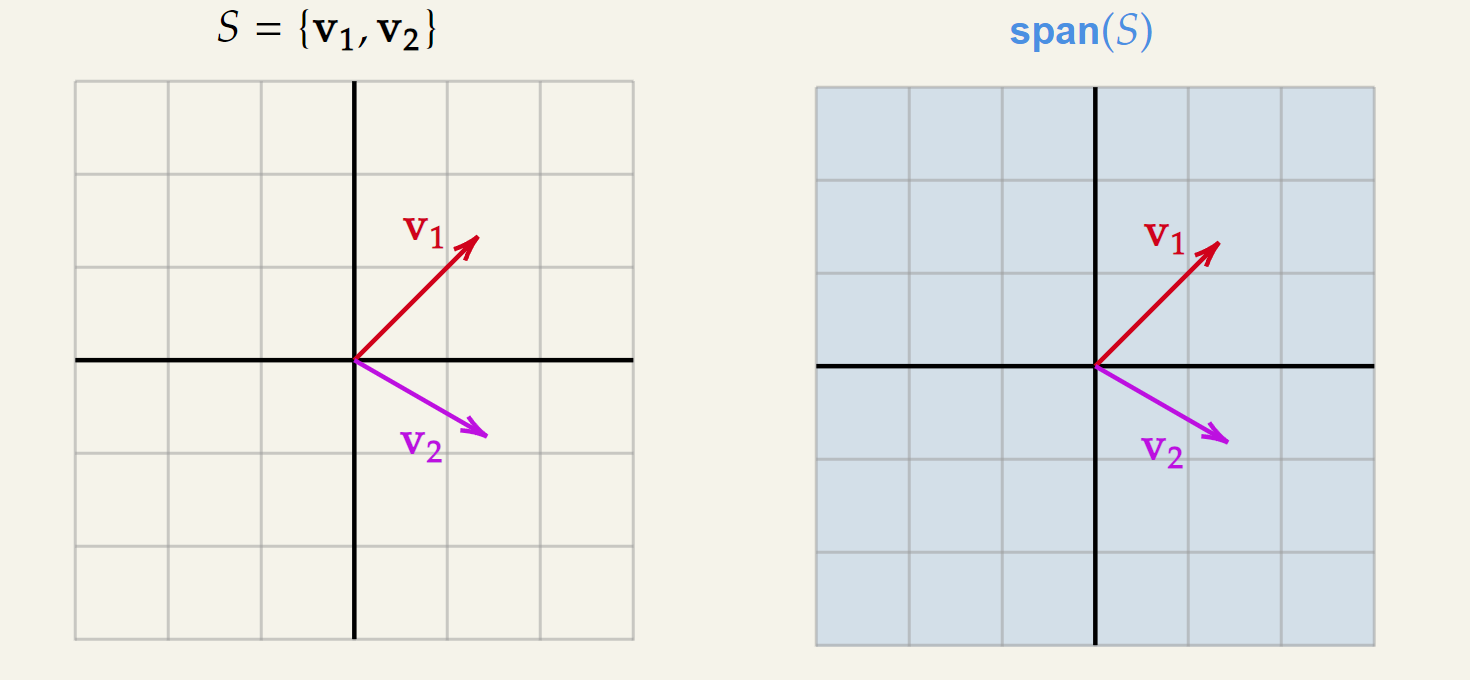
This means by taking the linear combination of ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ , we can generate any vector in ${\mathbb{R}}^2$.

But what if ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ were along the same line ? What would happen then?

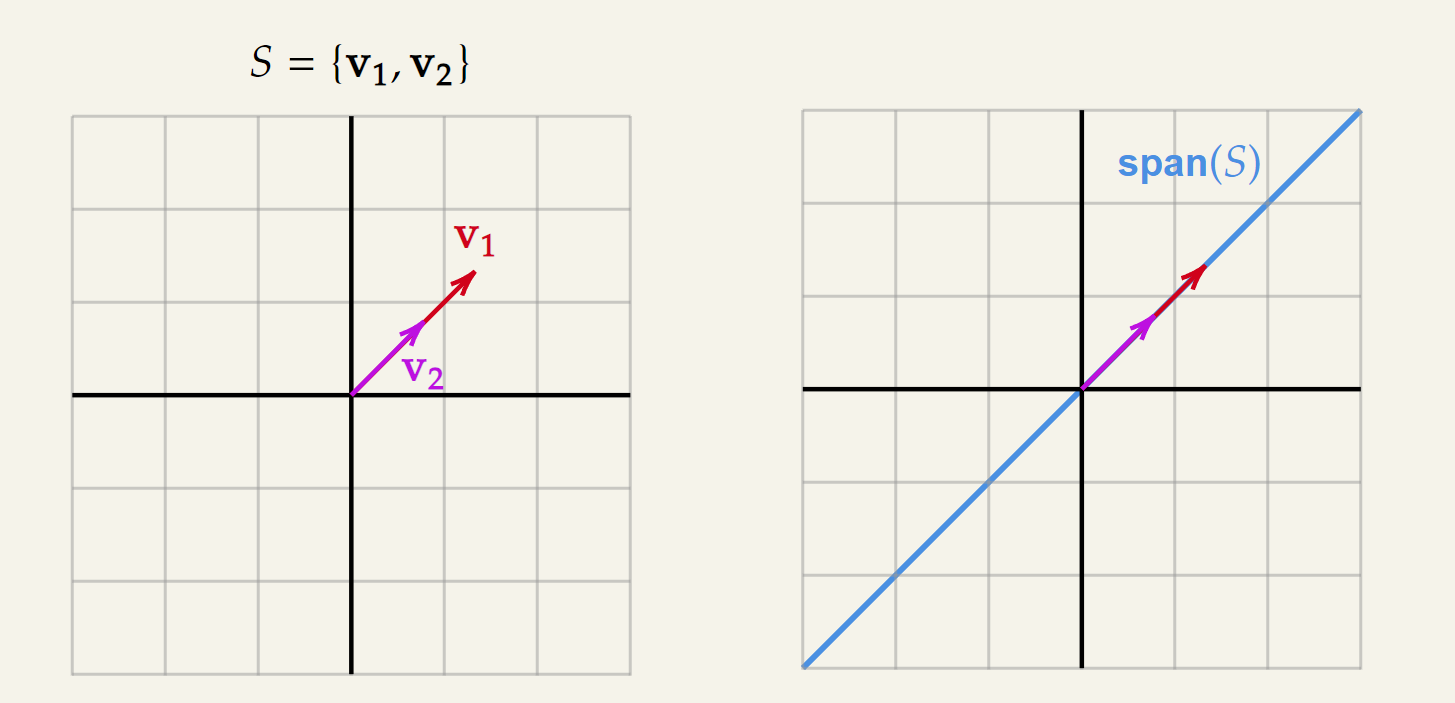
That will mean ${\mathbf{v}}_1$ is in the span of ${\mathbf{v}}_2$. The converse is also true i.e. ${\mathbf{v}}_2$ is in the span of ${\mathbf{v}}_1$. Any linear combination of these two vectors will only generate vectors that stay along a single line. Another way to say it is ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ are linearly dependent.

Consider the following visualization:

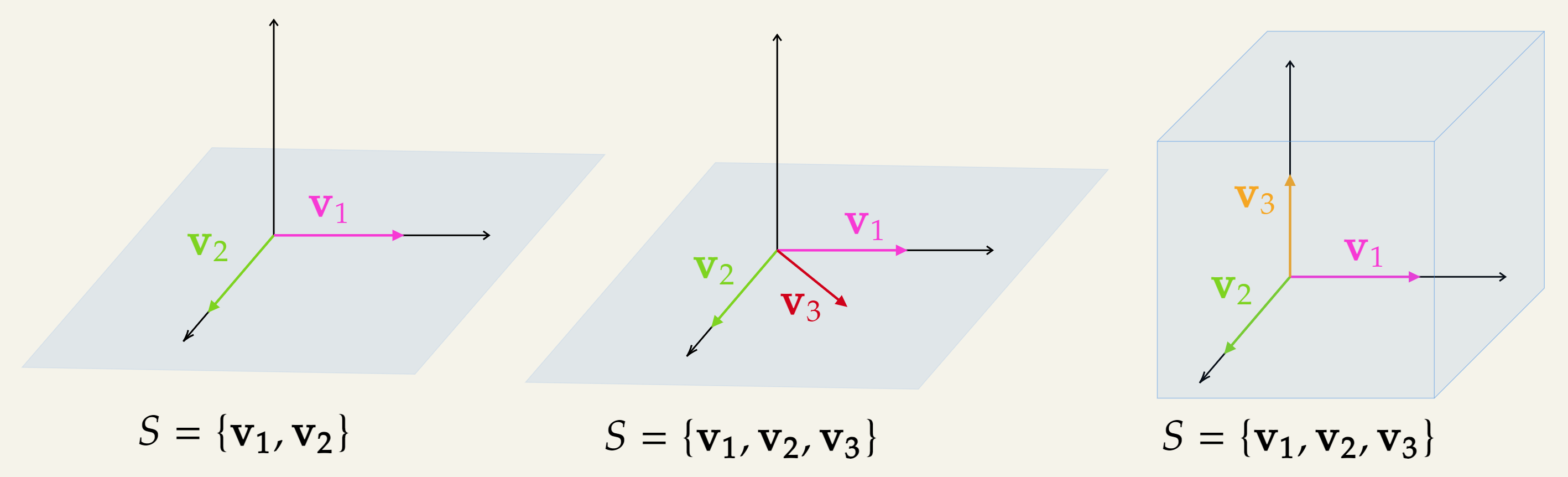
• In the first diagram, the span of ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ is a plane.
• In second diagram, we included another vector ${\mathbf{v}}_3$ , but ${\mathbf{v}}_3$ is in the span of ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$.
• In the third diagram, ${\mathbf{v}}_3$ is not in the span of ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$. Hence, ${\mathbf{v}}_1$, ${\mathbf{v}}_2$ and ${\mathbf{v}}_3$ are linearly independent to each other.

Relation between span and subspace

1. The span of any nonempty set of vectors is a subspace.
2. Every subspace is the span of some set of vectors.

Spanning Set §

Spanning set is a specific set of vectors from a vector space. When we take the linear combination of those vectors it spans the entire vector space. For example in ${\mathbb{R}}^3$, one example of spanning set is $\{{\mathbf{e}}_1,{\mathbf{e}}_2,{\mathbf{e}}_3\}$. It is possible to write any vector in ${\mathbb{R}}^3$ as linear combination of the spanning set $\{{\mathbf{e}}_1,{\mathbf{e}}_2,{\mathbf{e}}_3\}$.

Similarly in ${\mathbb{R}}^2$ an example of spanning set is $\{{\mathbf{e}}_1,{\mathbf{e}}_2\}$.

This can be generalized as follows. Consider a set of vectors $S=\{{\mathbf{v}}_1,{\mathbf{v}}_2,\cdots ,{\mathbf{v}}_n\}$ which is a subset of a vector space ${\mathbb{C}}^n$. The set $S$ is called the spanning set if every vector in ${\mathbb{C}}^n$ can be generated by taking a linear combination of vectors from $S$. We typically refer to it as ” $S$ spans ${\mathbb{C}}^n$ “.

Word of Caution:

The idea of spanning set is closely related with the idea of basis. But they are two distinct concepts. From the discussion above, it might seem to you that basis vectors form the spanning set, but it is not true in general. For example, the following set is a spanning set for ${\mathbb{R}}^2$ . Notice that every though they form a spanning set, the vectors in the set are not linearly independent.

$$\left\{\left[\begin{array}{c}1\\ 0\end{array}\right],\left[\begin{array}{c}0\\ 1\end{array}\right],\left[\begin{array}{c}1\\ 1\end{array}\right]\right\}$$

References §

1. Bernstein, Matthew. Span and Linear Independence. 11 June 2022, mbernste.github.io/posts/linear_independence/.