Latent Variable Model (LVM)

Latent variable models defines a distribution over observations $x$ by using a latent variable $z$. There are $5$ separate distributions associated with a LVM.

• $p(x,z)$ : Joint distribution of observation $x$ and latent variable $z$
• $p(z)$ : Prior distribution of latent variable $z$
• $p(x)$ : Marginal distribution of the observations $x$ (also known as evidence)
• $p(x \mid z)$ : Likelihood distribution $x$ given $z$
• $p(z\mid x)$ : Posterior distribution $z$ given $x$

A visualization is shown below:

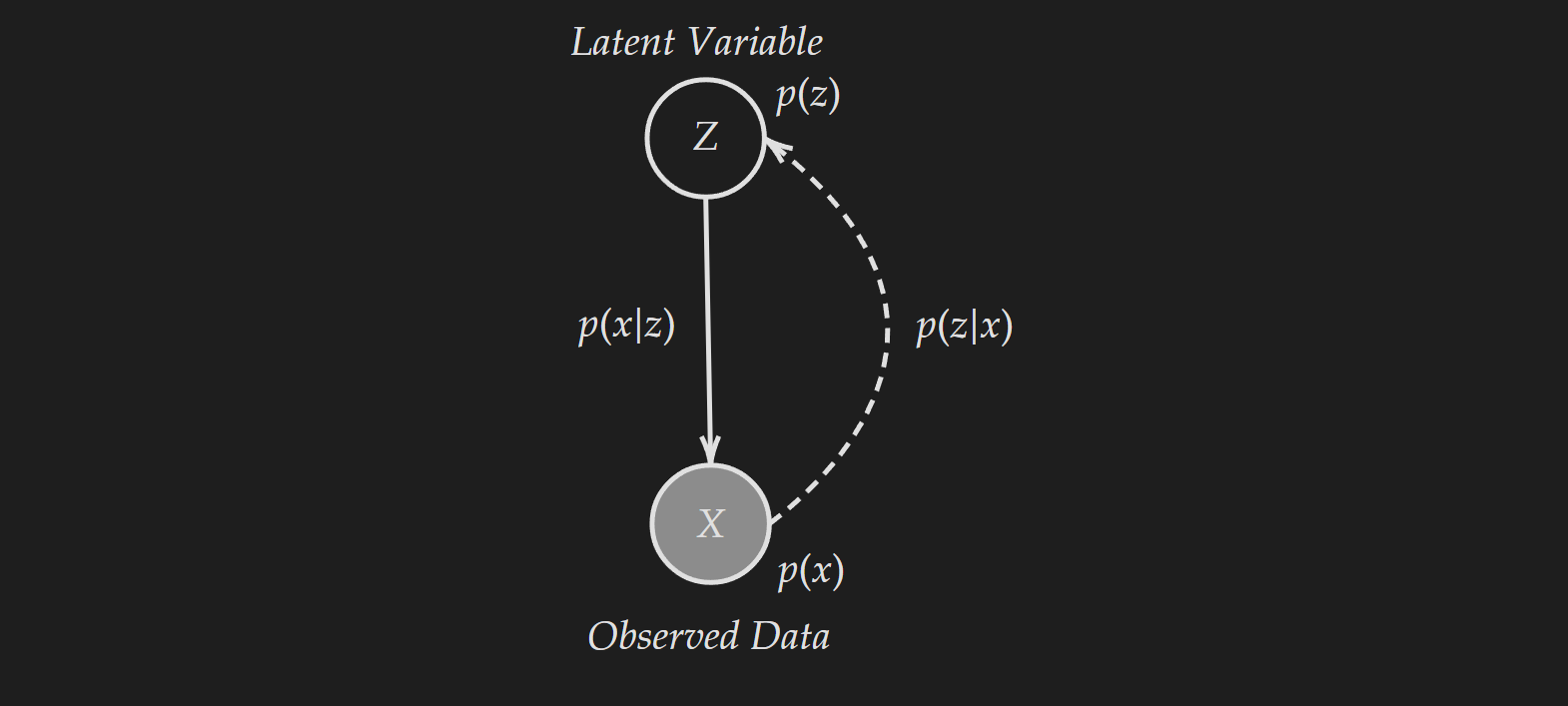Probabilistic Graphical Model (PGM) Representation of Latent Variable Models

We can get the joint distribution $p(x,z)$ if we know prior of the latent variable $p(z)$ and the conditional distribution $p(x \mid z)$.

\[p(x,z) = p(x \mid z ) p(z)\]

To get the posterior distribution we need to do the following. Note that this requires knowing the marginal distribution $p(x)$ by integrating over all possibilities of $z$ and the joint distribution $p(x,z)$.

\[p(z \mid x)=\frac{p(x,z)}{p(x)}=\frac{p(x, z)}{\int_z p(x, z) d z} = \frac{p(x\mid z) p(z)}{\int_z p(x\mid z) \ p(z)}\]

From this explanation you might think that the goal of latent variable models is to learn the posterior distribution $p(z \mid x)$. That’s correct, but there is a sub-goal which is learning the marginal distribution $p(x)= \int_z p(x, z) d z = \int_z p(x\mid z) \ p(z)$.

In practice calculating this term is intractable. The reason is in high dimensional space the integration becomes really hard and there is no closed form solution. Trying to solve it with computational methods is also hard. The popular way to get around it is to use variational inference methods to approximate $p(x)$ with another distribution.

Now this sub-goal sometimes becomes important in generative models. Because most of the time $p(x)$ is a complicated distribution in higher dimensional space. But $p(x \mid z )$ and $p(z)$ are “easy” distribution. So, with these two easy distribution we can learn a complicated distribution $p(x)$.

References

[1] Standford Online (2023). Stanford CS330 I Variational Inference and Generative Models l 2022 I Lecture 11. [online] www.youtube.com. Available at: https://www.youtube.com/watch?v=iL1c1KmYPM0.